Теплопроводность в бесконечном стержне
Рассмотрим процесс распространения тепла в бесконечном стержне. Для этого решается однородное уравнение
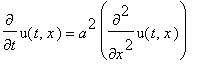
с начальным условием
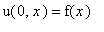 .
.
| > |
restart;with(PDETools):
|
Однородное уравнение и его решение
методом разделения переменных
:
| > |
PDE:=diff(u(t,x),t)=a^2*diff(u(t,x),x,x);
struc:=pdsolve(PDE,HINT=T(t)*X(x));
|
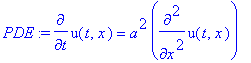
![struc := `&where`(u(t,x) = T(t)*X(x),[{diff(X(x),`$`(x,2)) = _c[1]*X(x)/a^2, diff(T(t),t) = _c[1]*T(t)}])](images/maple415.gif)
| > |
dsolve(diff(T(t),t)=_c[1]*T(t));
dsolve(diff(X(x),`$`(x,2))=_c[1]*X(x)/a^2);
|
![T(t) = _C1*exp(_c[1]*t)](images/maple416.gif)
![X(x) = _C1*exp(_c[1]^(1/2)/a*x)+_C2*exp(-_c[1]^(1/2)/a*x)](images/maple417.gif)
Сделаем замену постоянной разделения переменных:
![_c[1]](images/maple418.gif) = = -
= = -
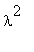
| > |
dsolve(diff(T(t),t)=-lambda^2*T(t)*a^2);
dsolve(diff(X(x),`$`(x,2))=-lambda^2*X(x));
|
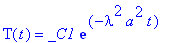
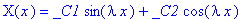
В результате общее решение имеет вид:
| > |
u(t,x):=(C1*sin(lambda*x)+C2*cos(lambda*x))*exp(-lambda^2*a^2*t);
|
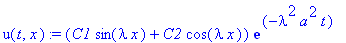
Функция
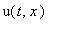 - есть решение уравнения для любого
- есть решение уравнения для любого
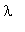 (где
(где
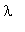 - непрерывно меняющейся параметр со значениями в интервале от -
- непрерывно меняющейся параметр со значениями в интервале от -
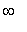 до +
до +
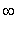 ), причем для каждого
), причем для каждого
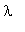 будут соответствующие коэффициенты
будут соответствующие коэффициенты
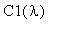 и
и
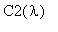 .
.
Поэтому имеем:
| > |
u[lambda](t,x):=(C1(lambda)*sin(lambda*x)+C2(lambda)*cos(lambda*x))*exp(-lambda^2*a^2*t);
|
 := (C1(lambda)*sin(lambda*x)+C2(lambda)*cos(lambda*x))*exp(-lambda^2*a^2*t)](images/maple431.gif)
В результате решение линейного обнородного уравнения можно представить в виде суперпозиции решений, зависящих от параметра
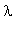 :
:
| > |
u(t,x):=int(u[lambda](t,x), lambda=-infinity..infinity);
|
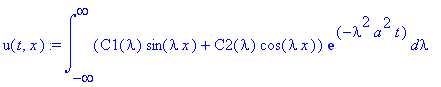
Для определения коэффициентов
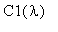 и
и
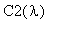 воспользуемся начальными условиями:
воспользуемся начальными условиями:
| > |
u_0(t,x):=eval(subs(t=0, u(t,x)))=f(x);
|
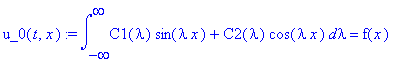
Это выражение соответсвует разложению функции
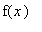 в интеграл Фурье:
в интеграл Фурье:
| > |
f(x)=(1/(2*Pi))*int(int(f(xi)*cos(lambda*(xi-x)),xi=-infinity..infinity),lambda=-infinity..infinity);
|
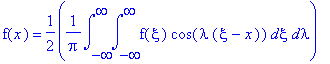
Значит, коэффициенты
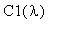 и
и
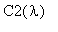 выражаются:
выражаются:
| > |
C1(lambda):=(1/(2*Pi))*int(f(xi)*sin(lambda*xi),xi=-infinity..infinity);
C2(lambda):=(1/(2*Pi))*int(f(xi)*cos(lambda*xi),xi=-infinity..infinity);
|
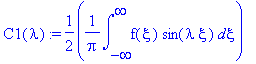
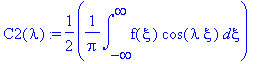
| > |
u(t,x):=int((C1(lambda)*sin(lambda*x)+C2(lambda)*cos(lambda*x))*exp(-lambda^2*a^2*t),lambda = -infinity .. infinity);
u(t,x):=combine(int((C1(lambda)*sin(lambda*x)+C2(lambda)*cos(lambda*x))*exp(-lambda^2*a^2*t),lambda = -infinity .. infinity));
|
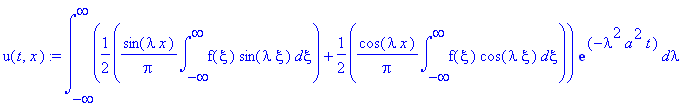
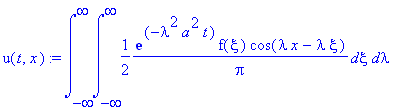
Полученное выражение можно преобразовать.
Для этого рассмотрим интеграл:
| > |
int(exp(-lambda^2*a^2*t)*cos(-lambda*x+lambda*xi), lambda = -infinity .. infinity);
|
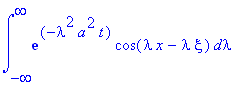
Сделаем замену переменной и преобразование подинтегральной функции:
| > |
simplify(subs({xi=-v*a*t^(1/2)+x,lambda=w/(a*sqrt(t))},exp(-lambda^2*a^2*t)*cos(-lambda*x+lambda*xi)));
|
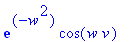
| > |
Int(exp(-lambda^2*a^2*t)*cos(-lambda*x+lambda*xi),lambda = -infinity .. infinity)=(1/(a*sqrt(t)))*int(exp(-w^2)*cos(w*v),w = -infinity .. infinity);
|
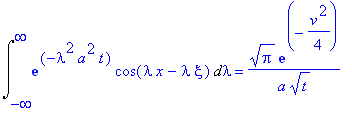
| > |
Int(exp(-lambda^2*a^2*t)*cos(-lambda*x+lambda*xi),lambda=-infinity..infinity)= subs(v=(x-xi)/a/t^(1/2),1/a/t^(1/2)*Pi^(1/2)*exp(-1/4*v^2));
|
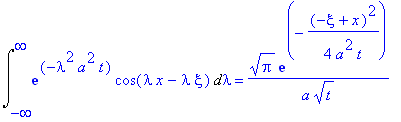
В результате решение примет вид:
| > |
u(t,x):=(1/(2*a*sqrt(Pi*t)))*int(f(xi)*exp(-1/4*(x-xi)^2/a^2/t),xi = -infinity .. infinity);
|
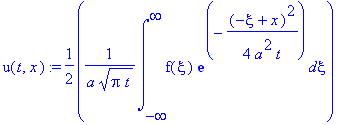
ПРИМЕР 1
Решить однородное уравнение
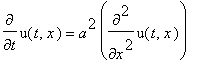
с начальным условияем
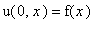 ,
,
где функция
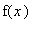 задана в виде:
задана в виде:
| > |
a:=1;L:=1;alpha:=1;l:=L/3;
f(xi):=u0*exp(-gamma^2*xi^2);
|
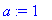
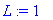
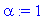
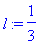
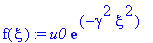
| > |
u0:=1;gamma:=0.5;
plot(f(xi), xi=-15..15, color=red,thickness=3);
|
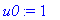
Error, attempting to assign to `gamma` which is protected
![[Maple Plot]](images/maple459.gif)
Для решения воспользуемся полученной в пункте 1.1. формулой:
| > |
u(t,x):=1/2*1/a/(Pi*t)^(1/2)*int(f(xi)*exp(-1/4*(x-xi)^2/a^2/t),xi = -infinity .. infinity);
|
![u(t,x) := 1/2*1/(Pi*t)^(1/2)*PIECEWISE([2*exp(1/(-4*gamma^2*t-1)*x^2*gamma^2)*u0/((4*gamma^2*t+1)/t)^(1/2)*Pi^(1/2), csgn(gamma^2+1/(4*t)) = 1],[infinity, otherwise])](images/maple460.gif)
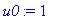
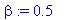
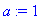
Решение уравнения:
| > |
with(plots):
u(t,x):=(1/(2*a*sqrt(Pi*t)))*exp(1/(-4*beta^2*a^2*t-1)*x^2*beta^2)*u0/((4*beta^2*a^2*t+1)/a^2/t)^(1/2);
|
Warning, the name changecoords has been redefined
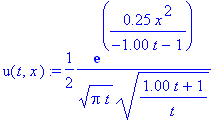
Представим полученные решения в виде двумерных анимированных графиков:
| > |
animate(plot,[u(t,x),x=-15..15], t=0.0001..60, frames=30,thickness=3);
|
![[Maple Plot]](images/maple465.gif)
Представим полученное решение в виде двумерных графиков для нескольких моментов времени:
| > |
tau:=60:
u_1(x):=subs(t=tau*0.000001,u(t,x)):
u_2(x):=subs(t=tau*(1/8),u(t,x)):
u_3(x):=subs(t=tau*(2/8),u(t,x)):
u_4(x):=subs(t=tau*(3/8),u(t,x)):
u_5(x):=subs(t=tau*(4/8),u(t,x)):
u_6(x):=subs(t=tau*(5/8),u(t,x)):
u_7(x):=subs(t=tau*(6/8),u(t,x)):
u_8(x):=subs(t=tau*(7/8),u(t,x)):
plot(u_1(x),x=-15..15,y=-0.02..0.3,title="t = 0", color=red,thickness=3);
plot(u_2(x),x=-15..15,y=-0.02..0.3,title="t = 1/8*tau",color=red,thickness=3);
plot(u_3(x),x=-15..15,y=-0.02..0.3,title="t = 2/8*tau",color=red,thickness=3);
plot(u_4(x),x=-15..15,y=-0.02..0.3,title="t = 3/8*tau",color=red,thickness=3);
plot(u_5(x),x=-15..15,y=-0.02..0.3,title="t = 4/8*tau",color=red,thickness=3);
plot(u_6(x),x=-15..15,y=-0.02..0.3,title="t = 5/8*tau",color=red,thickness=3);
plot(u_7(x),x=-15..15,y=-0.02..0.3,title="t = 6/8*tau",color=red,thickness=3);
plot(u_8(x),x=-15..15,y=-0.02..0.3,title="t = 7/8*tau",color=red,thickness=3);
|
![[Maple Plot]](images/maple466.gif)
![[Maple Plot]](images/maple467.gif)
![[Maple Plot]](images/maple468.gif)
![[Maple Plot]](images/maple469.gif)
![[Maple Plot]](images/maple470.gif)
![[Maple Plot]](images/maple471.gif)
![[Maple Plot]](images/maple472.gif)
![[Maple Plot]](images/maple473.gif)
ПРИМЕР 2
Решить однородное уравнение
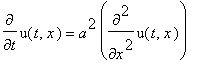
с начальным условияем
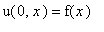 ,
,
где функция
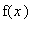 задана в виде:
задана в виде:
| > |
a:=1;L:=2;alpha:=1;
f(x):=x->piecewise(x<-L,0, x<0,alpha*(1+x/L),x<L,alpha*(1-x/L), x>L,0);
|
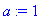
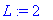
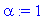
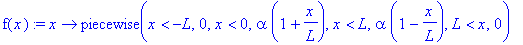
| > |
plot(f(x),-10..10,-0.1..1.1, numpoints=400,color=blue,thickness=3);
|
![[Maple Plot]](images/maple481.gif)
| > |
restart;
f(xi):=xi->piecewise(xi<-L,0, xi<0,alpha*(1+xi/L),xi<L,alpha*(1-xi/L), x>L,0);
|
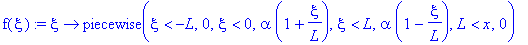
Для решения воспользуемся полученной в пункте 1.1. формулой:
| > |
u(t,x):=simplify(1/2*1/a/(Pi*t)^(1/2)*int(alpha*(1+xi/L)*exp(-1/4*(x-xi)^2/a^2/t),xi = -L .. 0)+1/2*1/a/(Pi*t)^(1/2)*int(alpha*(1-xi/L)*exp(-1/4*(x-xi)^2/a^2/t),xi = 0 .. L));
|
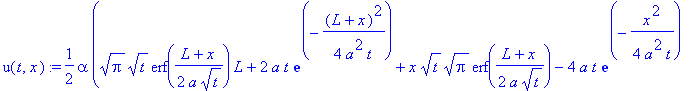
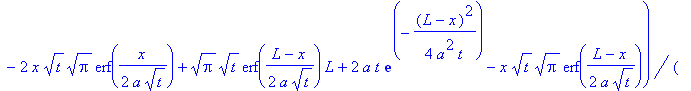
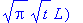
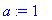
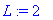
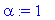
Представим полученные решения в виде двумерных анимированных графиков:
| > |
with(plots):
u(t,x):=-1/2*alpha*(-Pi^(1/2)*t^(1/2)*erf(1/2*(L+x)/a/t^(1/2))*L-2*a*t*exp(-1/4*(L+x)^2/a^2/t)-t^(1/2)*x*Pi^(1/2)*erf(1/2*(L+x)/a/t^(1/2))+4*a*t*exp(-1/4/a^2/t*x^2)+2*t^(1/2)*x*Pi^(1/2)*erf(1/2/a/t^(1/2)*x)-Pi^(1/2)*t^(1/2)*erf(1/2*(L-x)/a/t^(1/2))*L-2*a*t*exp(-1/4*(L-x)^2/a^2/t)+t^(1/2)*x*Pi^(1/2)*erf(1/2*(L-x)/a/t^(1/2)))/Pi^(1/2)/t^(1/2)/L;
animate(plot,[u(t,x),x=-15..15], t=0.0001..15, frames=30,thickness=3);
|
Warning, the name changecoords has been redefined
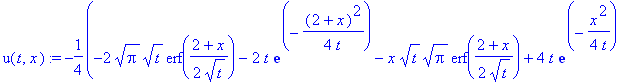
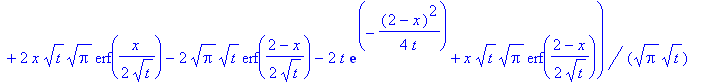
![[Maple Plot]](images/maple491.gif)
ПРИМЕР 3
Решить однородное уравнение
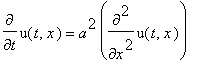
с начальным условияем
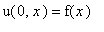 ,
,
где функция
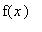 задана в виде:
задана в виде:
| > |
a:=1;L:=2;alpha:=1;
f(x):=x->piecewise(x<-L,0, x<L,alpha, x>L,0);
|
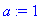
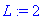
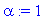
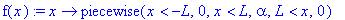
| > |
plot(f(x),-10..10,-0.1..1.1, numpoints=400,color=blue,thickness=3);
|
![[Maple Plot]](images/maple499.gif)
| > |
f(xi):=xi->piecewise(xi<-L,0, xi<L,alpha, xi>L,0);
|
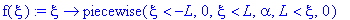
Для решения воспользуемся полученной в пункте 1.1. формулой:
| > |
u(t,x):=simplify(1/2*1/a/(Pi*t)^(1/2)*int(f(xi)*exp(-1/4*(x-xi)^2/a^2/t),xi = -L .. L));
|
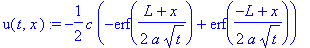
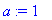
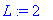
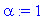
Решение уравнения:
| > |
with(plots):
u(t,x) := 1/2*(erf(1/2*(L+x)/a/t^(1/2))+erf(1/2*(L-x)/a/t^(1/2)));
|
Warning, the name changecoords has been redefined
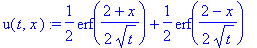
Представим полученные решения в виде двумерных анимированных графиков:
| > |
animate(plot,[u(t,x),x=-15..15], t=0.0001..15, frames=30,thickness=3);
|
![[Maple Plot]](images/maple506.gif)
Теплопроводность в полубесконечном стержне
Рассмотрим процесс распространения тепла в полубесконечном стержне. Для этого решается однородное уравнение
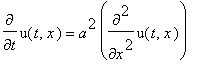
с начальным условием
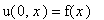
и граничным условием:
1. Конец стержня в точке
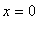 теплоизолирован:
теплоизолирован:
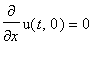 .
.
или
2. Конец стержня в точке
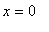 поддерживается при постоянной температуре:
поддерживается при постоянной температуре:
Однородное уравнение и его решение
методом разделения переменных
:
| > |
PDE:=diff(u(t,x),t)=a^2*diff(u(t,x),x,x);
struc:=pdsolve(PDE,HINT=T(t)*X(x));
|
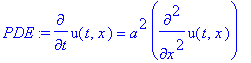
![struc := `&where`(u(t,x) = T(t)*X(x),[{diff(X(x),`$`(x,2)) = _c[1]*X(x)/a^2, diff(T(t),t) = _c[1]*T(t)}])](images/maple514.gif)
| > |
dsolve(diff(T(t),t)=_c[1]*T(t));
dsolve(diff(X(x),`$`(x,2))=_c[1]*X(x)/a^2);
|
![T(t) = _C1*exp(_c[1]*t)](images/maple515.gif)
![X(x) = _C1*exp(_c[1]^(1/2)/a*x)+_C2*exp(-_c[1]^(1/2)/a*x)](images/maple516.gif)
Сделаем замену постоянной разделения переменных:
![_c[1]](images/maple517.gif) = = -
= = -
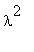
| > |
dsolve(diff(T(t),t)=-lambda^2*T(t)*a^2);
dsolve(diff(X(x),`$`(x,2))=-lambda^2*X(x));
|
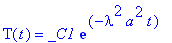
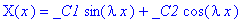
В результате общее решение имеет вид:
| > |
u(t,x):=(C1*sin(lambda*x)+C2*cos(lambda*x))*exp(-lambda^2*a^2*t);
|
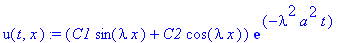
Функция
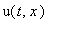 - есть решение уравнения для любого
- есть решение уравнения для любого
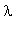 (где
(где
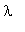 - непрерывно меняющейся параметр со значениями в интервале от -
- непрерывно меняющейся параметр со значениями в интервале от -
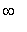 до +
до +
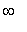 ), причем для каждого
), причем для каждого
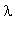 будут соответствующие коэффициенты
будут соответствующие коэффициенты
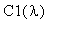 и
и
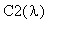 .
.
Поэтому имеем:
| > |
u[lambda](t,x):=(C1(lambda)*sin(lambda*x)+C2(lambda)*cos(lambda*x))*exp(-lambda^2*a^2*t);
|
 := (C1(lambda)*sin(lambda*x)+C2(lambda)*cos(lambda*x))*exp(-lambda^2*a^2*t)](images/maple530.gif)
В результате решение линейного обнородного уравнения можно представить в виде суперпозиции решений, зависящих от параметра
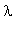 :
:
| > |
u(t,x):=int(u[lambda](t,x), lambda=-infinity..infinity);
|
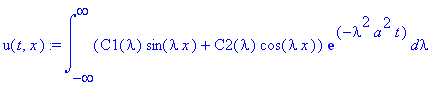
Для определения коэффициентов
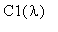 и
и
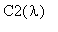 воспользуемся начальными условиями:
воспользуемся начальными условиями:
| > |
u_0(t,x):=eval(subs(t=0, u(t,x)))=f(x);
|
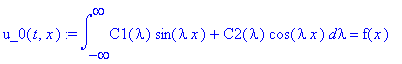
Это выражение соответсвует разложению функции
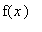 в интеграл Фурье:
в интеграл Фурье:
| > |
f(x)=(1/(2*Pi))*int(int(f(xi)*cos(lambda*(xi-x)),xi=-infinity..infinity),lambda=-infinity..infinity);
|
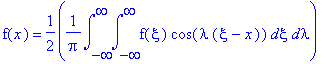
Значит, коэффициенты
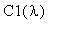 и
и
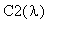 выражаются:
выражаются:
| > |
C1(lambda):=(1/(2*Pi))*int(f(xi)*sin(lambda*xi),xi=-infinity..infinity);
C2(lambda):=(1/(2*Pi))*int(f(xi)*cos(lambda*xi),xi=-infinity..infinity);
|
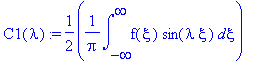
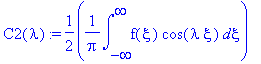
| > |
u(t,x):=int((C1(lambda)*sin(lambda*x)+C2(lambda)*cos(lambda*x))*exp(-lambda^2*a^2*t),lambda = -infinity .. infinity);
u(t,x):=combine(int((C1(lambda)*sin(lambda*x)+C2(lambda)*cos(lambda*x))*exp(-lambda^2*a^2*t),lambda = -infinity .. infinity));
|
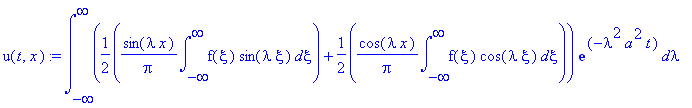
Error, (in depends/internal) too many levels of recursion
Полученное выражение можно преобразовать.
Для этого рассмотрим интеграл:
| > |
int(exp(-lambda^2*a^2*t)*cos(-lambda*x+lambda*xi), lambda = -infinity .. infinity);
|
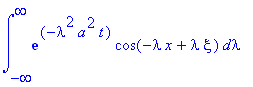
Сделаем замену переменной и преобразование подинтегральной функции:
| > |
simplify(subs({xi=-v*a*t^(1/2)+x,lambda=w/(a*sqrt(t))},exp(-lambda^2*a^2*t)*cos(-lambda*x+lambda*xi)));
|
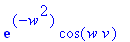
| > |
Int(exp(-lambda^2*a^2*t)*cos(-lambda*x+lambda*xi),lambda = -infinity .. infinity)=(1/(a*sqrt(t)))*int(exp(-w^2)*cos(w*v),w = -infinity .. infinity);
|
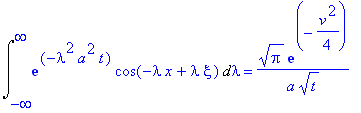
| > |
Int(exp(-lambda^2*a^2*t)*cos(-lambda*x+lambda*xi),lambda=-infinity..infinity)= subs(v=(x-xi)/a/t^(1/2),1/a/t^(1/2)*Pi^(1/2)*exp(-1/4*v^2));
|
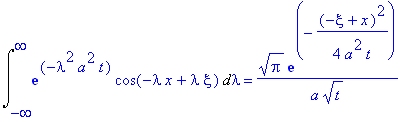
В результате решение примет вид:
| > |
u(t,x):=(1/(2*a*sqrt(Pi*t)))*int(f(xi)*exp(-1/4*(x-xi)^2/a^2/t),xi = -infinity .. infinity);
|
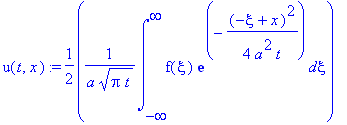
В случае полубесконечного стержня необходимо учесть граничное условие в точке
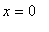 .
.
1
. Конец стержня в точке
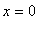 теплоизолирован:
теплоизолирован:
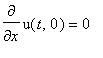 .
.
В этом случае
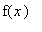 необходимо продолжить на отрицательную полуось четным образом:
необходимо продолжить на отрицательную полуось четным образом:
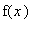 =
=
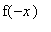 .
.
| > |
u_x(t,x):=diff(u(t,x),x);
|
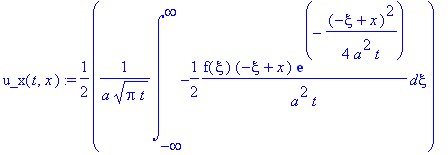
Сделаем замену переменной:
| > |
u0_x:=subs(x=0,u_x(t,x));
|
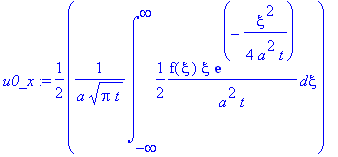
Здесь подинтегральная функция нечтна; поэтому интеграл равен нулю и граничное условие в точке
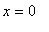 выполнено.
выполнено.
При этом решение может быть записано в виде:
| > |
u(t,x):=1/2*1/a/(Pi*t)^(1/2)*int(f(xi)*(exp(-1/4*(-xi+x)^2/a^2/t)+exp(-1/4*(xi+x)^2/a^2/t)),xi=-infinity..infinity);
|
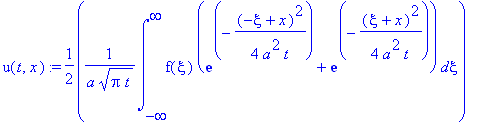
2
. Конец стержня в точке
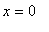 поддерживается при постоянной температуре (
поддерживается при постоянной температуре (
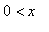 ):
):
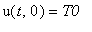 .
.
Для решения этой задачи преобразуем граничное условие к однородному :
| > |
U(t,x)=u(t,x)-T0;
F(x)=f(x)-T0;
|
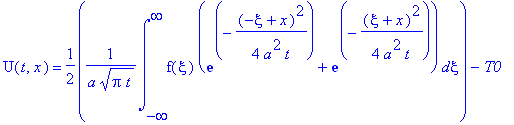
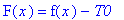
При этом
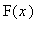 необходимо продолжить на отрицательную полуось нечетным образом:
необходимо продолжить на отрицательную полуось нечетным образом:
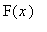 =
=
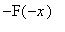 .
.
В этом случае решение задачи - функция:
| > |
U(t,x):=1/2*1/a/(Pi*t)^(1/2)*int(F(xi)*exp(-1/4*(-xi+x)^2/a^2/t),xi = -infinity .. infinity);
|
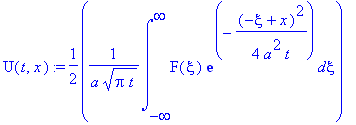
В результате имеем:
| > |
F(xi):=f(xi)-T0;
u(t,x):=T0+1/2*1/a/(Pi*t)^(1/2)*int((f(xi)+T0)*exp(-1/4*(-xi+x)^2/a^2/t),xi = -infinity .. infinity);
|
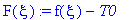
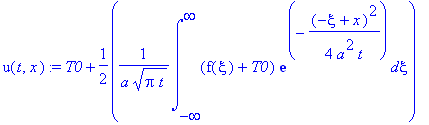
Учитывая нечетность функции
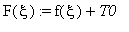 , получаем:
, получаем:
| > |
u(t,x):=T0+1/2*1/a/(Pi*t)^(1/2)*int((f(xi)-T0)*exp(-1/4*(-xi+x)^2/a^2/t),xi = -infinity .. 0)+1/2*1/a/(Pi*t)^(1/2)*int((f(xi)-T0)*exp(-1/4*(xi+x)^2/a^2/t),xi = 0 .. infinity);
|
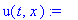
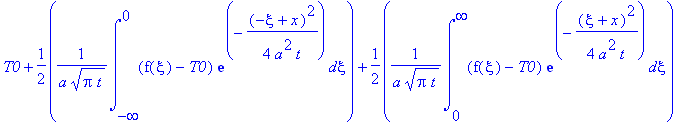
или
| > |
u(t,x):=T0+1/2*1/a/(Pi*t)^(1/2)*int((f(xi))*(exp(-1/4*(-xi+x)^2/a^2/t)-exp(-1/4*(xi+x)^2/a^2/t)),xi=0..infinity)-T0*Integr;
|
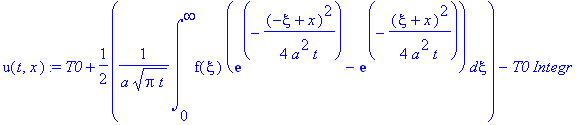
где:
| > |
Integr:=1/2/a/(Pi*t)^(1/2)*Int((T0)*exp(-1/4*(-xi+x)^2/a^2/t),xi = -infinity .. 0)-1/2/a/(Pi*t)^(1/2)*Int((T0)*exp(-1/4*(xi+x)^2/a^2/t),xi = 0 .. infinity);
|
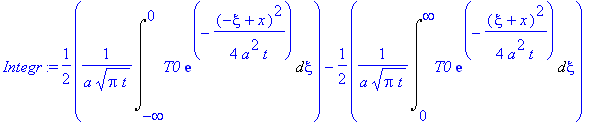
Для вычисления этих интегралов сделаем замены:
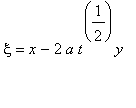 ,
,
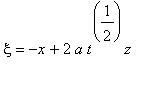 .
.
| > |
subs(xi=x-2*a*t^(1/2)*y,exp(-1/4*(-xi+x)^2/a^2/t));
subs(xi=-x+2*a*t^(1/2)*y,exp(-1/4*(xi+x)^2/a^2/t));
|
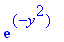
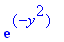
| > |
I1:=simplify((1/a/(Pi*t)^(1/2))*int(exp(-y^2),y = -infinity .. x/(2*a*t^(1/2)))*2*a*t^(1/2))/2;
I2:=simplify((1/a/(Pi*t)^(1/2))*int(exp(-y^2),y = x/(2*a*t^(1/2)) ..infinity)*2*a*t^(1/2))/2;
|
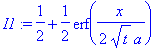
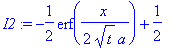
| > |
Integr:=simplify(I1-I2);
|
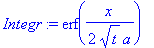
Таким образом, имеем:
| > |
u(t,x):=collect(T0+1/2*1/a/(Pi*t)^(1/2)*int((f(xi))*(exp(-1/4*(-xi+x)^2/a^2/t)-exp(-1/4*(xi+x)^2/a^2/t)),xi=0..infinity)-T0*Integr,T0);
|
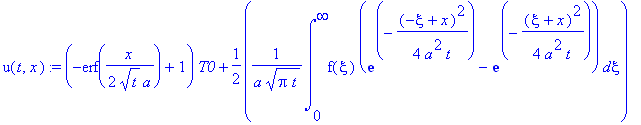
ПРИМЕР 1
Решить однородное уравнение
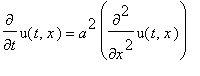
с граничным условием (конец стержня в точке
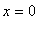 теплоизолирован):
теплоизолирован):
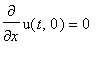 .
.
и начальным условияем
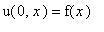 ,
,
где функция
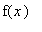 задана в виде:
задана в виде:
| > |
a:=1;l:=4;L:=6;alpha:=1;
f(x):=x->piecewise(x<l,0, x<L,alpha, x>L,0);
|
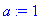
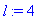
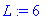
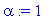
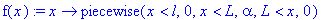
| > |
plot(f(x),0..10,-0.1..1.1, numpoints=400,color=blue,thickness=3);
|
![[Maple Plot]](images/maple592.gif)
| > |
restart;
f(xi):=xi->piecewise(xi<l,0, xi<L,alpha, xi>L,0);
|
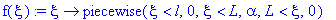
Для решения воспользуемся полученной в пункте 1.2. (граничное условие 1) формулой:
| > |
u(t,x):=simplify(1/2*1/a/(Pi*t)^(1/2)*int(f(xi)*(exp(-1/4*(-xi+x)^2/a^2/t)+exp(-1/4*(xi+x)^2/a^2/t)),xi = l .. L));
|
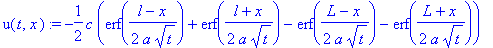
| > |
a:=1;l:=4;L:=6;alpha:=1;
|
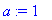
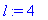
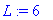
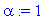
Решение уравнения:
| > |
with(plots):
u(t,x):=-1/2*(erf(1/2*(l-x)/a/t^(1/2))+erf(1/2*(l+x)/a/t^(1/2))+erf(1/2*(-L+x)/a/t^(1/2))-erf(1/2*(L+x)/a/t^(1/2)));
|
Warning, the name changecoords has been redefined
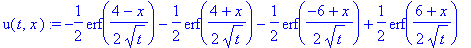
Представим полученные решения в виде двумерных анимированных графиков:
| > |
animate(plot,[u(t,x),x=0..15], t=0.00000001..12, frames=60,thickness=3);
|
![[Maple Plot]](images/maple600.gif)
Представим полученное решение в виде двумерных графиков для нескольких моментов времени:
| > |
tau:=12:
u_1(x):=subs(t=tau*0.000001,u(t,x)):
u_2(x):=subs(t=tau*(1/8),u(t,x)):
u_3(x):=subs(t=tau*(2/8),u(t,x)):
u_4(x):=subs(t=tau*(3/8),u(t,x)):
u_5(x):=subs(t=tau*(4/8),u(t,x)):
u_6(x):=subs(t=tau*(5/8),u(t,x)):
u_7(x):=subs(t=tau*(6/8),u(t,x)):
u_8(x):=subs(t=tau*(7/8),u(t,x)):
plot(u_1(x),x=0..15,y=-0.02..1.1,title="t = 0", color=red,thickness=3);
plot(u_2(x),x=0..15,y=-0.02..1.1,title="t = 1/8*tau",color=red,thickness=3);
plot(u_3(x),x=0..15,y=-0.02..1.1,title="t = 2/8*tau",color=red,thickness=3);
plot(u_4(x),x=0..15,y=-0.02..1.1,title="t = 3/8*tau",color=red,thickness=3);
plot(u_5(x),x=0..15,y=-0.02..1.1,title="t = 4/8*tau",color=red,thickness=3);
plot(u_6(x),x=0..15,y=-0.02..1.1,title="t = 5/8*tau",color=red,thickness=3);
plot(u_7(x),x=0..15,y=-0.02..1.1,title="t = 6/8*tau",color=red,thickness=3);
plot(u_8(x),x=0..15,y=-0.02..1.1,title="t = 7/8*tau",color=red,thickness=3);
|
![[Maple Plot]](images/maple601.gif)
![[Maple Plot]](images/maple602.gif)
![[Maple Plot]](images/maple603.gif)
![[Maple Plot]](images/maple604.gif)
![[Maple Plot]](images/maple605.gif)
![[Maple Plot]](images/maple606.gif)
![[Maple Plot]](images/maple607.gif)
![[Maple Plot]](images/maple608.gif)
ПРИМЕР 2
Решить однородное уравнение
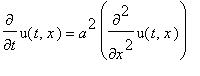
с граничным условием (конец стержня в точке
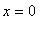 поддерживается при постоянной температуре (
поддерживается при постоянной температуре (
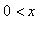 ):
):
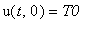
и начальным условияем
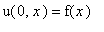 ,
,
где функция
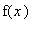 задана в виде:
задана в виде:
| > |
T0:=0; a:=1;l:=4;L:=6;alpha:=1;
f(x):=x->piecewise(x<l,T0, x<L,alpha+T0, x>L,0);
|
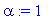
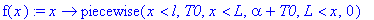
| > |
plot(f(x),0..10,-0.1..1.1, numpoints=400,color=blue,thickness=3);
|
![[Maple Plot]](images/maple621.gif)
| > |
restart;
f(xi):=xi->piecewise(xi<l,T0, xi<L,alpha+T0, xi>L,0);
|
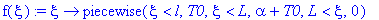
Для решения воспользуемся полученной в пункте 1.2. (граничное условие 2) формулой:
| > |
u(t,x):=simplify((-erf(1/2*x/a/t^(1/2))+1)*T0+1/2*1/a/(Pi*t)^(1/2)*int(f(xi)*(exp(-1/4*(-xi+x)^2/a^2/t)-exp(-1/4*(xi+x)^2/a^2/t)),xi = l .. L));
|
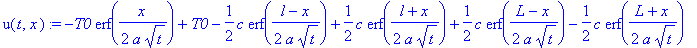
| > |
T0:=0; a:=1;l:=4;L:=6;alpha:=1;
|
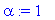
Решение уравнения:
| > |
with(plots):
u(t,x):=-T0*erf(1/2*x/a/t^(1/2))+T0+1/2*erf(1/2*(-l+x)/a/t^(1/2))+1/2*erf(1/2*(l+x)/a/t^(1/2))+1/2*erf(1/2*(L-x)/a/t^(1/2))-1/2*erf(1/2*(L+x)/a/t^(1/2));
|
Warning, the name changecoords has been redefined
Представим полученные решения в виде двумерных анимированных графиков:
| > |
animate(plot,[u(t,x),x=0..15, y=-0.1..1.1], t=0.0000001..12, frames=60,thickness=3);
|
![[Maple Plot]](images/maple630.gif)
Представим полученное решение в виде двумерных графиков для нескольких моментов времени:
| > |
tau:=12:
u_1(x):=subs(t=tau*0.000001,u(t,x)):
u_2(x):=subs(t=tau*(1/8),u(t,x)):
u_3(x):=subs(t=tau*(2/8),u(t,x)):
u_4(x):=subs(t=tau*(3/8),u(t,x)):
u_5(x):=subs(t=tau*(4/8),u(t,x)):
u_6(x):=subs(t=tau*(5/8),u(t,x)):
u_7(x):=subs(t=tau*(6/8),u(t,x)):
u_8(x):=subs(t=tau*(7/8),u(t,x)):
plot(u_1(x),x=0..15,y=-0.02..1.1,title="t = 0", color=red,thickness=3);
plot(u_2(x),x=0..15,y=-0.02..1.1,title="t = 1/8*tau",color=red,thickness=3);
plot(u_3(x),x=0..15,y=-0.02..1.1,title="t = 2/8*tau",color=red,thickness=3);
plot(u_4(x),x=0..15,y=-0.02..1.1,title="t = 3/8*tau",color=red,thickness=3);
plot(u_5(x),x=0..15,y=-0.02..1.1,title="t = 4/8*tau",color=red,thickness=3);
plot(u_6(x),x=0..15,y=-0.02..1.1,title="t = 5/8*tau",color=red,thickness=3);
plot(u_7(x),x=0..15,y=-0.02..1.1,title="t = 6/8*tau",color=red,thickness=3);
plot(u_8(x),x=0..15,y=-0.02..1.1,title="t = 7/8*tau",color=red,thickness=3);
|
![[Maple Plot]](images/maple631.gif)
![[Maple Plot]](images/maple632.gif)
![[Maple Plot]](images/maple633.gif)
![[Maple Plot]](images/maple634.gif)
![[Maple Plot]](images/maple635.gif)
![[Maple Plot]](images/maple636.gif)
![[Maple Plot]](images/maple637.gif)
![[Maple Plot]](images/maple638.gif)
Теплопроводность в конечном стержне
Рассмотрим процесс распространения тепла в полубесконечном стержне. Для этого решается однородное уравнение
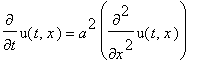
с начальным условием
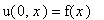
и граничными условиями:
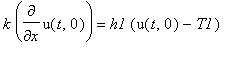
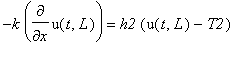
(
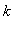 - коэффициент теплопроводности,
- коэффициент теплопроводности,
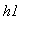 и
и
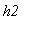 - коэффициенты теплообмена на концах стержня,
- коэффициенты теплообмена на концах стержня,
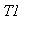 и
и
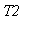 - темпетатуры на концах стержня).
- темпетатуры на концах стержня).
Однородное уравнение и его решение
методом разделения переменных
:
| > |
PDE:=diff(u(t,x),t)=a^2*diff(u(t,x),x,x);
struc:=pdsolve(PDE,HINT=T(t)*X(x));
|
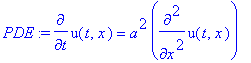
![struc := `&where`(u(t,x) = T(t)*X(x),[{diff(X(x),`$`(x,2)) = _c[1]*X(x)/a^2, diff(T(t),t) = _c[1]*T(t)}])](images/maple649.gif)
| > |
dsolve(diff(T(t),t)=_c[1]*T(t));
dsolve(diff(X(x),`$`(x,2))=_c[1]*X(x)/a^2);
|
![T(t) = _C1*exp(_c[1]*t)](images/maple650.gif)
![X(x) = _C1*exp(_c[1]^(1/2)/a*x)+_C2*exp(-_c[1]^(1/2)/a*x)](images/maple651.gif)
Сделаем замену постоянной разделения переменных:
![_c[1]](images/maple652.gif) = = -
= = -
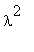
| > |
dsolve(diff(T(t),t)=-lambda^2*T(t)*a^2);
dsolve(diff(X(x),`$`(x,2))=-lambda^2*X(x));
|
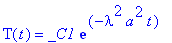
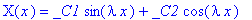
В результате общее решение имеет вид:
| > |
u(t,x):=(C1*sin(lambda*x)+C2*cos(lambda*x))*exp(-lambda^2*a^2*t);
|
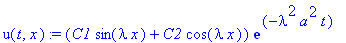
Начальное условие имеет вид:
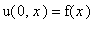 :
:
Граничные условия имеют вид (
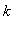 - коэффициент теплопроводности,
- коэффициент теплопроводности,
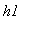 и
и
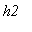 - коэффициенты теплообмена на концах стержня,
- коэффициенты теплообмена на концах стержня,
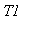 и
и
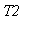 - темпетатуры на концах стержня)
- темпетатуры на концах стержня)
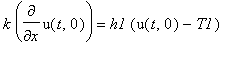
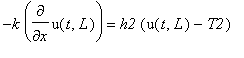
| > |
k*diff(u(t,x),x)=h1*(u(t,x)-T1);
-k*diff(u(t,x),x)=h2*(u(t,x)-T2);
|
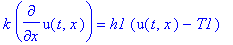
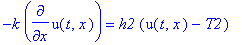
Чтобы применить метод Фурье, необходимо свести исходную задачу к случаю однородных граничных условий.
Для этого введем функцию
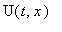 :
:
| > |
u(t,x):=U(t,x)+kappa+sigma*x;
|
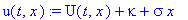
Здесь
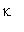 и
и
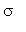 - постоянные коэффициенты.
- постоянные коэффициенты.
| > |
u_x(t,x):=diff(u(t,x),x);
|
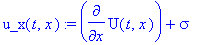
| > |
u_x(t,x) := U_x(t,x) +sigma;
|
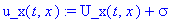
Гричные условия при этом запишутся:
| > |
subs(x=0,k*u_x(t,x)=h1*(u(t,x)-T1));
subs(x=L,-k*u_x(t,x)=h2*(u(t,x)-T2));
|
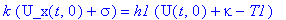
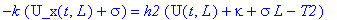
Поскольку для
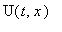 предполагаются однородные граничные условия, получаем:
предполагаются однородные граничные условия, получаем:
| > |
k*sigma=h1*(kappa-T1);
-k*sigma=h2*(kappa+sigma*L-T2);
|
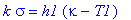
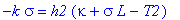
Отсюда имеем:
| > |
solve({k*sigma=h1*(kappa-T1),-k*sigma=h2*(kappa+sigma*L-T2)},{kappa,sigma});
|
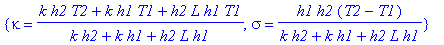
В этом случае граничные условия для
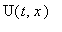 действительно примут вид однородных:
действительно примут вид однородных:
| > |
simplify(subs({x = 0, kappa = (k*h2*T2-k*h1*T1+h2*L*h1*T1)/(k*h2-k*h1+h2*L*h1), sigma = -h1*h2*(-T2+T1)/(k*h2-k*h1+h2*L*h1)},(U_x(t,0)+sigma-h1*(U(t,0)+kappa-T1)/k)*k = 0)); simplify(subs({x = 0, kappa = (k*h2*T2-k*h1*T1+h2*L*h1*T1)/(k*h2-k*h1+h2*L*h1), sigma = -h1*h2*(-T2+T1)/(k*h2-k*h1+h2*L*h1)},(U_x(t,L)-sigma+h2*(U(t,L)+kappa+sigma*L-T2)/k)*k = 0));
|

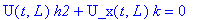
Начальное условие для
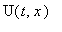 запишется:
запишется:
| > |
u(t,x):=U(t,x)+kappa+sigma*x;
subs(t=0,u(t,x)=f(x));
|
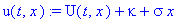
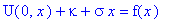
или
| > |
F(x)=f(x)-kappa-sigma*x;
subs(t=0,U(t,x)=F(x));
|
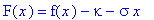
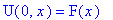
При этом функция
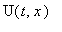 удовлетворяет тому же уравнению, что и
удовлетворяет тому же уравнению, что и
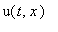 :
:
| > |
u(t,x):=U(t,x)+kappa+sigma*x;
diff(u(t,x),t)=a^2*diff(u(t,x),x,x);
diff(U(t,x),t)=a^2*diff(U(t,x),x,x);
|
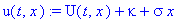
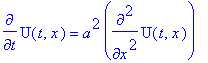
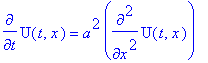
Поэтому для функция
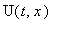 общее решение имеет вид:
общее решение имеет вид:
| > |
U(t,x):=(C1*sin(lambda*x)+C2*cos(lambda*x))*exp(-lambda^2*a^2*t);
|
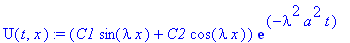
| > |
U_x(t,x):=diff(U(t,x),x);
|
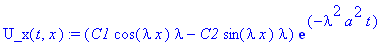
Учтем однородные граничные условия для
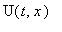 :
:
| > |
eval(subs(x=0,U(t,x)*k=h1*U_x(t,x)));
eval(subs(x=L,U(t,x)*k=-h2*U_x(t,x)));
|
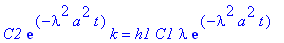
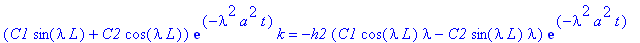
| > |
solve(C2*k=h1*C1*lambda,C1);
solve(C1*sin(lambda*L)+C2*cos(lambda*L)*k=-h2*(C1*cos(lambda*L)*lambda-C2*sin(lambda*L)*lambda),C1);
|
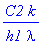
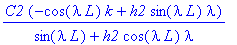
Отсюда имеем уравнение, определяющее
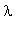 :
:
| > |
k/h1/lambda=-(cos(lambda*L)*k-h2*sin(lambda*L)*lambda)/(sin(lambda*L)+h2*cos(lambda*L)*lambda);
|
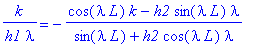
| > |
k/h1/lambda = -(k-h2*tan(lambda*L)*lambda)/(tan(lambda*L)+h2*lambda);
|
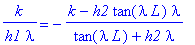
| > |
solve(k/h1/lambda = -(k-h2*G*lambda)/(G+h2*lambda), G);
|
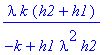
| > |
tan(lambda*L)=-k*lambda*(h1+h2)/(k-h1*lambda^2*h2);
|
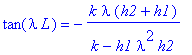
Рассмотрим несколько режимов.
1.
Концы стержня в одинаковом режиме; концы стержня теплоизолированы:
| > |
subs({h1=0, h2=0},tan(lambda*L) = -k*lambda*(h1+h2)/(k-h1*lambda^2*h2));
|
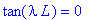
2.
Концы стержня в одинаковом режиме; температуры на концах постоянны:
| > |
restart;
limit(limit(tan(lambda*L) = -k*lambda*(h1+h2)/(k-h1*lambda^2*h2), h1=infinity), h2=infinity);
|
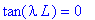
Значит, при одинаковых режимах на концах стержня
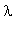 удовлетворяет уравнению:
удовлетворяет уравнению:
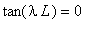 .
.
Откуда получаем:
| > |
_EnvAllSolutions := true:
solve(tan(lambda*L)=0,lambda);
|
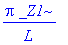
или, в обычном виде,
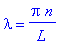
3.
Концы стержня в разных режимах; один конец стержня теплоизолирован, температура на втором конце постоянна:
| > |
restart;
limit(tan(lambda*L) = -k*lambda*(h1+h2)/(k-h1*lambda^2*h2), h1=0);
|
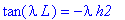
При h2 -->
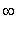 имеем:
имеем:
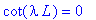
| > |
_EnvAllSolutions := true:
solve(cot(lambda*L)=0,lambda);
|
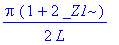
или, в обычном виде,
| > |
lambda=1/2*Pi*(1+2*n)/L;
|
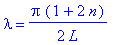
Для симметричного случая результат аналогичен.
Таим образом, общее решение для
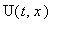 , соответствующее параметру
, соответствующее параметру
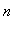 имеет вид:
имеет вид:
| > |
restart;
U[n](t,x):=(C1[n]*sin(lambda[n]*x)+C2[n]*cos(lambda[n]*x))*exp(-lambda[n]^2*a^2*t);
|
 := (C1[n]*sin(lambda[n]*x)+C2[n]*cos(lambda[n]*x))*exp(-lambda[n]^2*a^2*t)](images/maple718.gif)
Теперь определим коэффициенты и выпишем общие решения.
1.
Концы стержня в одинаковом режиме; концы стержня теплоизолированы:
| > |
lambda[n]:=Pi*n/L;
U[n](t,x):=(C1[n]*sin(lambda[n]*x)+C2[n]*cos(lambda[n]*x))*exp(-lambda[n]^2*a^2*t);
U_x[n](t,x):=diff(U[n](t,x),x);
|
![lambda[n] := Pi*n/L](images/maple719.gif)
 := (C1[n]*sin(Pi*n/L*x)+C2[n]*cos(Pi*n/L*x))*exp(-Pi^2*n^2/L^2*a^2*t)](images/maple720.gif)
 := (C1[n]*cos(Pi*n/L*x)*Pi*n/L-C2[n]*sin(Pi*n/L*x)*Pi*n/L)*exp(-Pi^2*n^2/L^2*a^2*t)](images/maple721.gif)
| > |
eval(subs(x=0,U_x[n](t,x)*k=0));
eval(subs(x=L,U_x[n](t,x)*k=0));
|
![C1[n]*Pi*n/L*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple722.gif)
![(C1[n]*cos(Pi*n)*Pi*n/L-C2[n]*sin(Pi*n)*Pi*n/L)*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple723.gif)
| > |
simplify((C1[n]*cos(Pi*n)*Pi*n/L-C2[n]*sin(Pi*n)*Pi*n/L)*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0) assuming n::integer;
|
![C1[n]*(-1)^n*Pi*n/L*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple724.gif)
Откуда:
![C1[n] = 0](images/maple725.gif)
| > |
U[n](t,x):=C2[n]*cos(lambda[n]*x)*exp(-lambda[n]^2*a^2*t);
|
 := C2[n]*cos(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t)](images/maple726.gif)
Общее решение имеемт вид:
| > |
U(t,x):=sum(U[n](t,x), n=0..infinity);
|
![U(t,x) := sum(C2[n]*cos(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t),n = 0 .. infinity)](images/maple727.gif)
| > |
eval(subs(t=0,U(t,x)=F(x)));
|
![sum(C2[n]*cos(Pi*n/L*x),n = 0 .. infinity) = F(x)](images/maple728.gif)
Поэтому коэффициенты
![C2[n]](images/maple729.gif) определяются согласно формулам преобразования Фурье:
определяются согласно формулам преобразования Фурье:
| > |
C2[n]:=(2/L)*int(F(xi)*cos(Pi*n/L*xi), xi=0..L);
|
![C2[n] := 2/L*int(F(xi)*cos(Pi*n/L*xi),xi = 0 .. L)](images/maple730.gif)
Выпишем общее решение.
| > |
F(xi):=f(xi);
U(t,x):=sum(C2[n]*cos(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t),n=0..infinity);
|
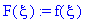
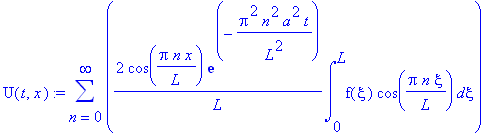
Таким образом, общее решение имеет вид:
| > |
u(t,x):=subs(F(xi)=f(xi),U(t,x));
|
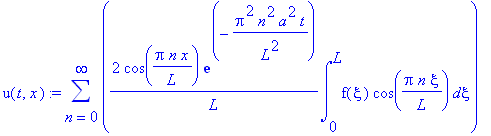
2.
Концы стержня в разных режимах.
| > |
lambda[n]:=Pi*n/L;
U[n](t,x):=(C1[n]*sin(lambda[n]*x)+C2[n]*cos(lambda[n]*x))*exp(-lambda[n]^2*a^2*t);
|
![lambda[n] := Pi*n/L](images/maple734.gif)
 := (C1[n]*sin(Pi*n/L*x)+C2[n]*cos(Pi*n/L*x))*exp(-Pi^2*n^2/L^2*a^2*t)](images/maple735.gif)
| > |
eval(subs(x=0,U[n](t,x)*k=0));
eval(subs(x=L,U[n](t,x)*k=0));
|
![C2[n]*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple736.gif)
![(C1[n]*sin(Pi*n)+C2[n]*cos(Pi*n))*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple737.gif)
| > |
simplify((C1[n]*sin(Pi*n)+C2[n]*cos(Pi*n))*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0) assuming n::integer;
|
![C2[n]*(-1)^n*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple738.gif)
Откуда:
![C2[n] = 0](images/maple739.gif)
| > |
U[n](t,x):=C1[n]*sin(lambda[n]*x)*exp(-lambda[n]^2*a^2*t);
|
 := C1[n]*sin(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t)](images/maple740.gif)
Общее решение имеемт вид:
| > |
U(t,x):=sum(U[n](t,x), n=0..infinity);
|
![U(t,x) := sum(C1[n]*sin(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t),n = 0 .. infinity)](images/maple741.gif)
| > |
eval(subs(t=0,U(t,x)=F(x)));
|
![sum(C1[n]*sin(Pi*n/L*x),n = 0 .. infinity) = F(x)](images/maple742.gif)
Поэтому коэффициенты
![C2[n]](images/maple743.gif) определяются согласно формклам преобразования Фурье:
определяются согласно формклам преобразования Фурье:
| > |
C1[n]:=(2/L)*int(F(xi)*cos(Pi*n/L*xi), xi=0..L);
|
![C1[n] := 2/L*int(F(xi)*cos(Pi*n/L*xi),xi = 0 .. L)](images/maple744.gif)
Выпишем общее решение.
| > |
F(xi):=f(xi);
U(t,x) := sum(C1[n]*sin(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t),n =0.. infinity);
|
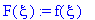
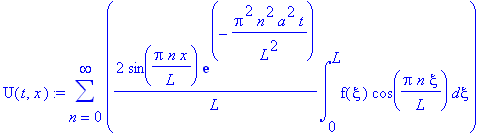
Таким образом, общее решение имеет вид:
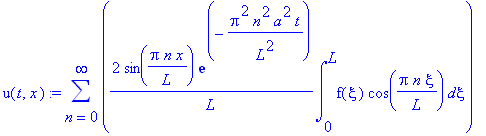
3.
Концы стержня в разных режимах.
| > |
lambda[n]:=1/2*Pi*(1+2*n)/L;
U[n](t,x):=(C1[n]*sin(lambda[n]*x)+C2[n]*cos(lambda[n]*x))*exp(-lambda[n]^2*a^2*t);
U_x[n](t,x):=diff(U[n](t,x),x);
|
![lambda[n] := 1/2*Pi*(1+2*n)/L](images/maple748.gif)
 := (C1[n]*sin(1/2*Pi*(1+2*n)/L*x)+C2[n]*cos(1/2*Pi*(1+2*n)/L*x))*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)](images/maple749.gif)
 := (1/2*C1[n]*cos(1/2*Pi*(1+2*n)/L*x)*Pi*(1+2*n)/L-1/2*C2[n]*sin(1/2*Pi*(1+2*n)/L*x)*Pi*(1+2*n)/L)*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)](images/maple750.gif)
 := (1/2*C1[n]*cos(1/2*Pi*(1+2*n)/L*x)*Pi*(1+2*n)/L-1/2*C2[n]*sin(1/2*Pi*(1+2*n)/L*x)*Pi*(1+2*n)/L)*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)](images/maple751.gif)
| > |
eval(subs(x=0,U_x[n](t,x)*k=0));
eval(subs(x=L,U[n](t,x)*k=0));
|
![1/2*C1[n]*Pi*(1+2*n)/L*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)*k = 0](images/maple752.gif)
![(C1[n]*sin(1/2*Pi*(1+2*n))+C2[n]*cos(1/2*Pi*(1+2*n)))*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)*k = 0](images/maple753.gif)
| > |
simplify((C1[n]*sin(1/2*Pi*(1+2*n))+C2[n]*cos(1/2*Pi*(1+2*n)))*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)*k = 0) assuming n::integer;
|
![C1[n]*(-1)^n*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)*k = 0](images/maple754.gif)
Откуда:
![C1[n] = 0](images/maple755.gif)
| > |
U[n](t,x):=C2[n]*cos(lambda[n]*x)*exp(-lambda[n]^2*a^2*t);
|
 := C2[n]*cos(1/2*Pi*(1+2*n)/L*x)*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)](images/maple756.gif)
Общее решение имеемт вид:
| > |
U(t,x):=sum(U[n](t,x), n=1..infinity);
|
![U(t,x) := sum(C2[n]*cos(1/2*Pi*(1+2*n)/L*x)*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t),n = 1 .. infinity)](images/maple757.gif)
| > |
eval(subs(t=0,U(t,x)=F(x)));
|
![sum(C2[n]*cos(1/2*Pi*(1+2*n)/L*x),n = 1 .. infinity) = F(x)](images/maple758.gif)
Поэтому коэффициенты
![C2[n]](images/maple759.gif) определяются согласно формклам преобразования Фурье:
определяются согласно формклам преобразования Фурье:
| > |
C2[n]:=(2/L)*int(F(xi)*cos(1/2*Pi*(1+2*n)/L*xi), xi=0..L);
|
![C2[n] := 2/L*int(F(xi)*cos(1/2*Pi*(1+2*n)/L*xi),xi = 0 .. L)](images/maple760.gif)
Выпишем общее решение.
| > |
h1:=0;
sigma:= -h1*h2*(-T2+T1)/(k*h2+k*h1+h2*L*h1);
kappa:= limit((k*h2*T2+k*h1*T1+h2*L*h1*T1)/(k*h2+k*h1+h2*L*h1), h2=infinity);
F(xi):=f(xi)-kappa-sigma*xi;
U(t,x) := sum(C2[n]*cos(1/2*Pi*(1+2*n)/L*x)*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t),n =0..infinity);
|
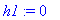
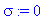
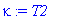
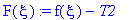
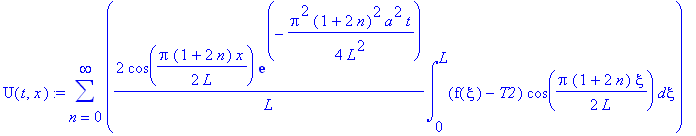
Таким образом, общее решение имеет вид:
| > |
u(t,x):=U(t,x)+kappa+sigma*x;
|
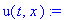
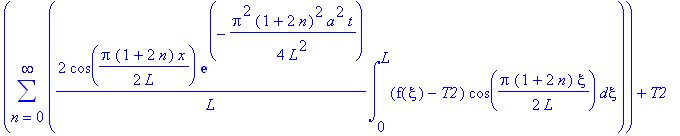
ПРИМЕР 1
Решить однородное уравнение
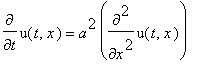
с граничным условием первого типа и начальным условием
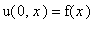 ,
,
где функция
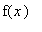 задана в виде:
задана в виде:
| > |
T0:=1; a:=1;L:=12;
f(x):=x->piecewise(x<L/2,T0, x<L,0);
|
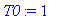
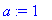
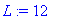
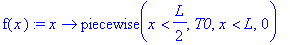
| > |
plot(f(x),0..12,-0.1..1.1, numpoints=400,color=blue,thickness=3);
|
![[Maple Plot]](images/maple775.gif)
| > |
restart;
f(xi):=xi->piecewise(xi<L/2,T0, xi<L,0);
|
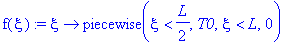
Для решения воспользуемся полученной в пункте 1.3. (граничное условие 1) формулой:
| > |
C2_0 := 2/L*int(T0,xi = 0 .. L/2);
u(t,x):=sum(2/L*cos(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t)*int(T0*cos(Pi*n/L*xi),xi=0..L/2),n = 0..infinity);
|
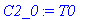
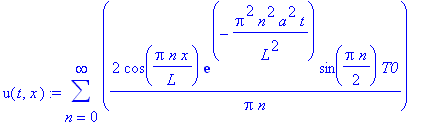
Поскольку
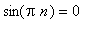 при
при
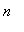 -->
-->
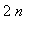
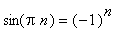 при
при
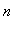 -->
-->
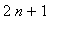
Решение уравнения:
| > |
u(t,x):=C2_0/2+sum(2*(-1)^n*cos(Pi*(2*n+1)/L*x)*exp(-Pi^2*(2*n+1)^2/L^2*a^2*t)*T0/Pi/(2*n+1),n=0..infinity);
|
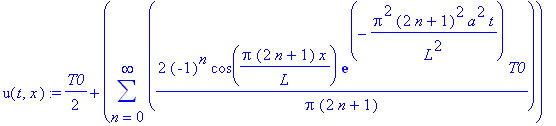
| > |
with(plots):
T0:=1; a:=1;L:=12;
u(t,x):=1/2*T0+sum(2*(-1)^n*cos(Pi*(2*n+1)/L*x)*exp(-Pi^2*(2*n+1)^2/L^2*a^2*t)*T0/Pi/(2*n+1),n=0..1000):
|
Warning, the name changecoords has been redefined
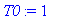
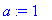
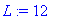
Представим полученные решения в виде двумерных анимированных графиков:
| > |
animate(plot,[u(t,x),x=0..12, y=-0.1..1.1], t=0.0001..30, frames=30,thickness=3);
|
![[Maple Plot]](images/maple789.gif)
ПРИМЕР 2
Решить однородное уравнение
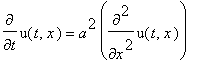
с граничным условием второго типа и начальным условияем
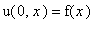 ,
,
где функция
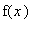 задана в виде:
задана в виде:
| > |
a:=1;L:=12;T0:=1;
f(x):=x->piecewise(x<L/2,2*T0*x/L,x<L,2*T0*(L-x)/L);
|
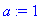
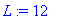
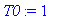
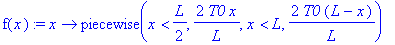
| > |
plot(f(x),0..12,-0.1..1.1, numpoints=400,color=blue,thickness=3);
|
![[Maple Plot]](images/maple797.gif)
| > |
restart;
f(xi):=xi->piecewise(xi<L/2,2*T0*xi/L,xi<L,2*T0*(L-xi)/L);
|
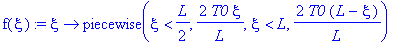
Для решения воспользуемся полученной в пункте 1.3. (граничное условие 2) формулой:
| > |
C2_0:=2/L*int(2*T0*xi/L,xi=0..L/2)+2/L*int(2*T0*(L-xi)/L,xi =L/2.. L);
u(t,x):=simplify(sum(2/L*cos(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t)*(int(2*T0*xi/L*cos(Pi*n/L*xi),xi= 0..L/2)+int(2*T0*(L-xi)/L*cos(Pi*n/L*xi),xi=L/2..L)),n=1..infinity));
|
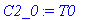
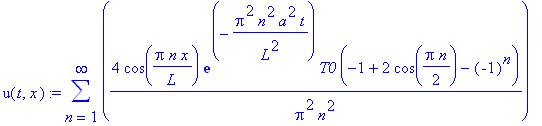
Поскольку
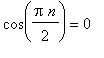 при
при
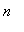 -->
-->
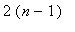
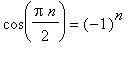 при
при
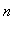 -->
-->
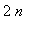
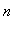 -->
-->
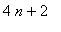
Решение уравнения:
| > |
u(t,x):=C2_0/2-sum(16*cos(Pi*(4*n+2)/L*x)*exp(-Pi^2*(4*n+2)^2/(L^2)*a^2*t)*T0/(Pi^2)/((4*n+2)^2),n =0..infinity);
|
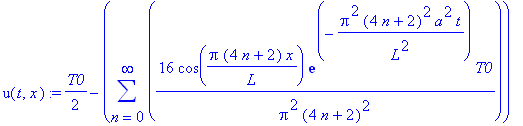
| > |
with(plots):
a:=1;L:=12;T0:=1;
u(t,x):=1/2*T0-sum(16*cos(Pi*(4*n+2)/L*x)*exp(-Pi^2*(4*n+2)^2/L^2*a^2*t)*T0/Pi^2/(4*n+2)^2,n=0..222):
|
Warning, the name changecoords has been redefined
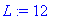
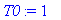
Представим полученные решения в виде двумерных анимированных графиков:
| > |
animate(plot,[u(t,x),x=0..12, y=-0.1..1.1], t=0..15, frames=30,thickness=3);
|
![[Maple Plot]](images/maple813.gif)
ПРИМЕР 3�
Решить однородное уравнение
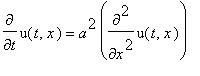
с граничным условием третьего типа и начальным условияем
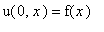 ,
,
где функция
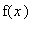 задана в виде:
задана в виде:
| > |
T0:=1; a:=1;L:=12;
f(x):=x->piecewise(x<L,T0);
|
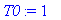
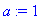
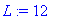

| > |
plot(f(x),0..13,-0.1..1.1, numpoints=400,color=blue,thickness=3);
|
![[Maple Plot]](images/maple821.gif)
| > |
restart;
f(x):=x->piecewise(x<L,T0);
|

Для решения воспользуемся полученной в пункте 1.3. (граничное условие 3) формулой:
| > |
u(t,x):=sum(2/L*cos(1/2*Pi*(1+2*n)/L*x)*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)*int((T0-T2)*cos(1/2*Pi*(1+2*n)/L*xi),xi = 0 .. L),n = 1 .. infinity)+T2;
|
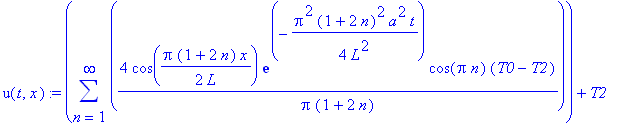
Поскольку
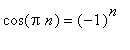
Решение уравнения:
| > |
u(t,x):=sum(4*cos(1/2*Pi*(1+2*n)/L*x)*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)*(-1)^n*(T0-T2)/Pi/(1+2*n),n=0..infinity)+T2;
|
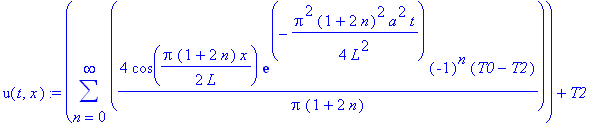
| > |
with(plots):
T0:=1; a:=1.5;L:=12;T2:=T0/4;
u(t,x):=sum(4*cos(1/2*Pi*(1+2*n)/L*x)*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)*(-1)^n*(T0-T2)/Pi/(1+2*n),n=0..1000)+T2:
|
Warning, the name changecoords has been redefined
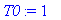
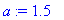
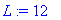
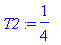
Представим полученные решения в виде двумерных анимированных графиков:
| > |
animate(plot,[u(t,x),x=0..12, y=-0.1..1.1], t=0.0001..30, frames=30,thickness=3);
|
![[Maple Plot]](images/maple830.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Maple Plot]](images/maple14.gif)
![[Maple Plot]](images/maple15.gif)
![[Maple Plot]](images/maple16.gif)
![[Maple Plot]](images/maple17.gif)
![[Maple Plot]](images/maple18.gif)
![[Maple Plot]](images/maple19.gif)
![[Maple Plot]](images/maple20.gif)
![[Maple Plot]](images/maple21.gif)
![[Maple Plot]](images/maple22.gif)
![[Maple Plot]](images/maple23.gif)
![]()
![]()
![[Maple Plot]](images/maple26.gif)
![a1 := `&where`(u(r,theta,phi) = _F1(r)*_F2(theta)*_F3(phi),[{diff(_F2(theta),`$`(theta,2)) = _c[2]/sin(theta)^2*_F2(theta)-_c[1]*_F2(theta)-cot(theta)*diff(_F2(theta),theta), diff(_F1(r),`$`(r,2)) = 1/...](images/maple28.gif)
![a1 := `&where`(u(r,theta,phi) = _F1(r)*_F2(theta)*_F3(phi),[{diff(_F2(theta),`$`(theta,2)) = _c[2]/sin(theta)^2*_F2(theta)-_c[1]*_F2(theta)-cot(theta)*diff(_F2(theta),theta), diff(_F1(r),`$`(r,2)) = 1/...](images/maple29.gif)
![a1 := `&where`(u(r,theta,phi) = _F1(r)*_F2(theta)*_F3(phi),[{diff(_F2(theta),`$`(theta,2)) = _c[2]/sin(theta)^2*_F2(theta)-_c[1]*_F2(theta)-cot(theta)*diff(_F2(theta),theta), diff(_F1(r),`$`(r,2)) = 1/...](images/maple30.gif)
![]()
![]()
![]()
![]()
![]()
![a3 := `&where`(u(r,theta,phi) = R(r)*Theta(theta)*Phi(phi),[{diff(Theta(theta),`$`(theta,2)) = _c[2]/sin(theta)^2*Theta(theta)-_c[1]*Theta(theta)-cot(theta)*diff(Theta(theta),theta), diff(R(r),`$`(r,2)...](images/maple36.gif)
![a3 := `&where`(u(r,theta,phi) = R(r)*Theta(theta)*Phi(phi),[{diff(Theta(theta),`$`(theta,2)) = _c[2]/sin(theta)^2*Theta(theta)-_c[1]*Theta(theta)-cot(theta)*diff(Theta(theta),theta), diff(R(r),`$`(r,2)...](images/maple37.gif)
![`&where`(u(r,theta,phi) = R(r)*Theta(theta)*Phi(phi),[{diff(Theta(theta),`$`(theta,2)) = _c[2]/sin(theta)^2*Theta(theta)-_c[1]*Theta(theta)-cot(theta)*diff(Theta(theta),theta), diff(R(r),`$`(r,2)) = 1/...](images/maple38.gif)
![`&where`(u(r,theta,phi) = R(r)*Theta(theta)*Phi(phi),[{diff(Theta(theta),`$`(theta,2)) = _c[2]/sin(theta)^2*Theta(theta)-_c[1]*Theta(theta)-cot(theta)*diff(Theta(theta),theta), diff(R(r),`$`(r,2)) = 1/...](images/maple39.gif)
![a2 := `&where`(u(x,r,phi) = _F1(r)*_F2(x)*_F3(phi),[{-(1-x^2)^(1/2)*(1/(1-x^2)^(1/2)*diff(_F2(x),x)*x-(1-x^2)^(1/2)*diff(_F2(x),`$`(x,2))) = _c[2]/(1-x^2)*_F2(x)-_c[1]*_F2(x)+x*diff(_F2(x),x), diff(_F1...](images/maple40.gif)
![a2 := `&where`(u(x,r,phi) = _F1(r)*_F2(x)*_F3(phi),[{-(1-x^2)^(1/2)*(1/(1-x^2)^(1/2)*diff(_F2(x),x)*x-(1-x^2)^(1/2)*diff(_F2(x),`$`(x,2))) = _c[2]/(1-x^2)*_F2(x)-_c[1]*_F2(x)+x*diff(_F2(x),x), diff(_F1...](images/maple41.gif)
![a2 := `&where`(u(x,r,phi) = _F1(r)*_F2(x)*_F3(phi),[{-(1-x^2)^(1/2)*(1/(1-x^2)^(1/2)*diff(_F2(x),x)*x-(1-x^2)^(1/2)*diff(_F2(x),`$`(x,2))) = _c[2]/(1-x^2)*_F2(x)-_c[1]*_F2(x)+x*diff(_F2(x),x), diff(_F1...](images/maple42.gif)
![`&where`(u(x,r,phi) = _F1(r)*_F2(x)*_F3(phi),[{-(1-x^2)^(1/2)*(1/(1-x^2)^(1/2)*diff(_F2(x),x)*x-(1-x^2)^(1/2)*diff(_F2(x),`$`(x,2))) = _c[2]/(1-x^2)*_F2(x)-_c[1]*_F2(x)+x*diff(_F2(x),x), diff(_F1(r),`$...](images/maple43.gif)
![`&where`(u(x,r,phi) = _F1(r)*_F2(x)*_F3(phi),[{-(1-x^2)^(1/2)*(1/(1-x^2)^(1/2)*diff(_F2(x),x)*x-(1-x^2)^(1/2)*diff(_F2(x),`$`(x,2))) = _c[2]/(1-x^2)*_F2(x)-_c[1]*_F2(x)+x*diff(_F2(x),x), diff(_F1(r),`$...](images/maple44.gif)
![`&where`(u(x,r,phi) = _F1(r)*_F2(x)*_F3(phi),[{-(1-x^2)^(1/2)*(1/(1-x^2)^(1/2)*diff(_F2(x),x)*x-(1-x^2)^(1/2)*diff(_F2(x),`$`(x,2))) = _c[2]/(1-x^2)*_F2(x)-_c[1]*_F2(x)+x*diff(_F2(x),x), diff(_F1(r),`$...](images/maple45.gif)
![]()
![[Maple Plot]](images/maple48.gif)
![[Maple Plot]](images/maple49.gif)
![]()
![[Maple Plot]](images/maple52.gif)
![[Maple Plot]](images/maple53.gif)
![[Maple Plot]](images/maple54.gif)
![[Maple Plot]](images/maple55.gif)
![]()
![]()
![[Maple Plot]](images/maple62.gif)
![[Maple Plot]](images/maple63.gif)
![[Maple Plot]](images/maple64.gif)
![[Maple Plot]](images/maple65.gif)
![[Maple Plot]](images/maple66.gif)
 .
.
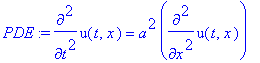
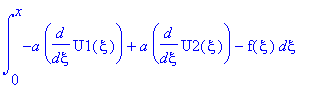
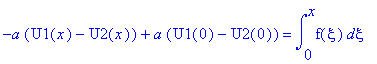
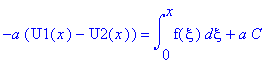
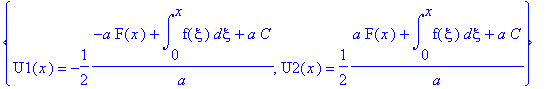
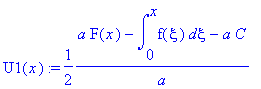
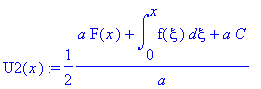
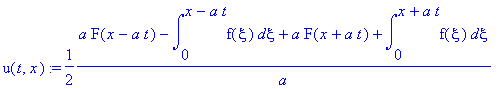
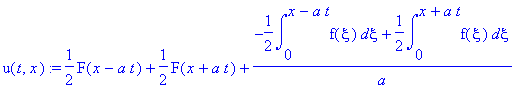
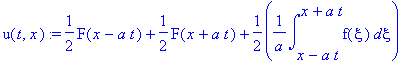
 .
.
![[Maple Plot]](images/maple99.gif)
![u(t,x) := 1/2*PIECEWISE([0, x-a*t < -L],[alpha*(1+(x-a*t)/L), x-a*t < 0],[alpha*(1-(x-a*t)/L), x-a*t < L],[0, L < x-a*t])+1/2*PIECEWISE([0, x+a*t < -L],[alpha*(1+(x+a*t)/L), x+a*t < 0],[alpha*(1-(x+a*t...](images/maple102.gif)
![u1(t,x) := 1/2*PIECEWISE([0, x-t < -1],[1+x-t, x-t < 0],[1-x+t, x-t < 1],[0, 1 < x-t])](images/maple106.gif)
![u2(t,x) := 1/2*PIECEWISE([0, x+t < -1],[1+x+t, x+t < 0],[1-x-t, x+t < 1],[0, 1 < x+t])](images/maple107.gif)
![u(t,x) := 1/2*PIECEWISE([0, x-t < -1],[1+x-t, x-t < 0],[1-x+t, x-t < 1],[0, 1 < x-t])+1/2*PIECEWISE([0, x+t < -1],[1+x+t, x+t < 0],[1-x-t, x+t < 1],[0, 1 < x+t])](images/maple108.gif)
![[Maple Plot]](images/maple109.gif)
![[Maple Plot]](images/maple110.gif)
![[Maple Plot]](images/maple111.gif)
![[Maple Plot]](images/maple112.gif)
![[Maple Plot]](images/maple113.gif)
![[Maple Plot]](images/maple114.gif)
![[Maple Plot]](images/maple115.gif)
![[Maple Plot]](images/maple116.gif)
![[Maple Plot]](images/maple117.gif)
![[Maple Plot]](images/maple118.gif)
![[Maple Plot]](images/maple119.gif)
![[Maple Plot]](images/maple120.gif)
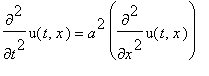
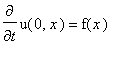 .
.
![[Maple Plot]](images/maple131.gif)
![u(t,x) := PIECEWISE([0, x-a*t < l1],[alpha, x-a*t < l2],[0, L < x-a*t])+PIECEWISE([0, x+a*t < l1],[alpha, x+a*t < l2],[0, L < x+a*t])](images/maple134.gif)
![u1(t,x) := PIECEWISE([0, x-t < -.8],[1, x-t < .8],[0, .8 < x-t])](images/maple140.gif)
![u2(t,x) := PIECEWISE([0, x+t < -.8],[1, x+t < .8],[0, .8 < x+t])](images/maple141.gif)
![u(t,x) := PIECEWISE([0, x-t < -.8],[1, x-t < .8],[0, .8 < x-t])+PIECEWISE([0, x+t < -.8],[1, x+t < .8],[0, .8 < x+t])](images/maple142.gif)
![[Maple Plot]](images/maple143.gif)
![[Maple Plot]](images/maple144.gif)
![[Maple Plot]](images/maple145.gif)
![[Maple Plot]](images/maple146.gif)
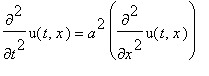
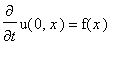 .
.
![[Maple Plot]](images/maple156.gif)
![f(xi) := PIECEWISE([0, xi < -L],[v0, xi < L],[0, L < xi])](images/maple157.gif)
![u(t,x) := 1/2*1/a*int(PIECEWISE([0, xi < -L],[v0, xi < L],[0, L < xi]),xi = x-a*t .. x+a*t)](images/maple159.gif)
![u(t,x) := 1/2*a*PIECEWISE([-v0*L, x < -L],[v0*x, x < L],[v0*L, L < x])](images/maple160.gif)
![u(t,x) := -1/2*a*PIECEWISE([-v0*L, x-a*t < -L],[v0*x-a*t, x-a*t < L],[v0*L, L < x-a*t])+1/2*a*PIECEWISE([-v0*L, x+a*t < -L],[v0*x+a*t, x+a*t < L],[v0*L, L < x+a*t])](images/maple161.gif)
![u1(t,x) := -1/2*PIECEWISE([-2, x-t < -2],[x-t, x-t < 2],[2, 2 < x-t])](images/maple167.gif)
![u2(t,x) := 1/2*PIECEWISE([-2, x+t < -2],[x+t, x+t < 2],[2, 2 < x+t])](images/maple168.gif)
![u(t,x) := -1/2*PIECEWISE([-2, x-t < -2],[x-t, x-t < 2],[2, 2 < x-t])+1/2*PIECEWISE([-2, x+t < -2],[x+t, x+t < 2],[2, 2 < x+t])](images/maple169.gif)
![[Maple Plot]](images/maple170.gif)
![[Maple Plot]](images/maple171.gif)
![[Maple Plot]](images/maple172.gif)
![[Maple Plot]](images/maple173.gif)
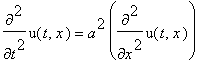
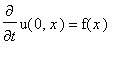 .
.
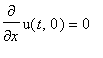 .
.
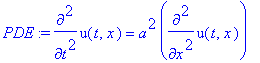
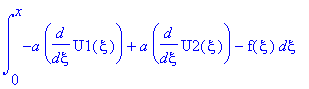
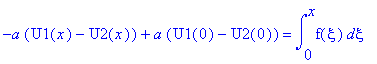

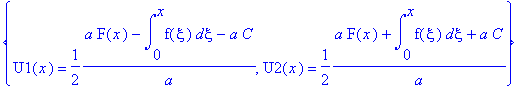
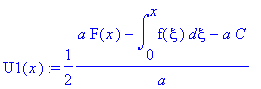
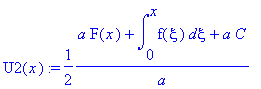
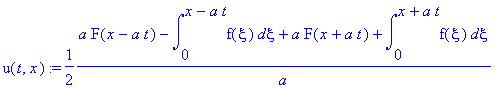
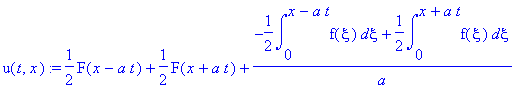
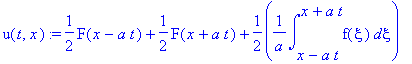
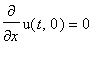 .
.
![u(t,x) := PIECEWISE([1/2*F(x-a*t)+1/2*F(x+a*t)+1/2*1/a*int(f(xi),xi = x-a*t .. x+a*t), t < x/a],[1/2*F(x+a*t)-1/2*F(-x+a*t)+1/2*1/a*int(f(xi),xi = -x+a*t .. x+a*t), x/a < t])](images/maple202.gif)
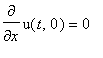
![u(t,x) := PIECEWISE([1/2*F(x-a*t)+1/2*F(x+a*t)+1/2*1/a*int(f(xi),xi = x-a*t .. x+a*t), t < x/a],[1/2*F(x-a*t)+F(x+a*t)+1/2*1/a*int(f(xi),xi = 0 .. x+a*t)+1/2*1/a*int(f(xi),xi = 0 .. x-a*t), x/a < t])](images/maple204.gif)
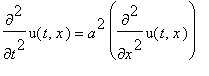
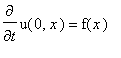 .
.
![[Maple Plot]](images/maple216.gif)
![u(t,x) := 1/2*PIECEWISE([0, x-a*t < -L-l],[alpha*(1+(x-a*t+l)/L), x-a*t < -l],[alpha*(1-(x-a*t+l)/L), x-a*t < L-l],[0, L-l < x-a*t])-1/2*PIECEWISE([0, x+a*t < -L+l],[alpha*(1+(x+a*t-l)/L), x+a*t < l],[...](images/maple219.gif)
![u1(t,x) := 1/2*PIECEWISE([0, x+t < 3],[-3+x+t, x+t < 4],[5-x-t, x+t < 5],[0, 5 < x+t])](images/maple224.gif)
![u2(t,x) := -1/2*PIECEWISE([0, x-t < -5],[5+x-t, x-t < -4],[-3-x+t, x-t < -3],[0, -3 < x-t])](images/maple225.gif)
![u(t,x) := 1/2*PIECEWISE([0, x+t < 3],[-3+x+t, x+t < 4],[5-x-t, x+t < 5],[0, 5 < x+t])-1/2*PIECEWISE([0, x-t < -5],[5+x-t, x-t < -4],[-3-x+t, x-t < -3],[0, -3 < x-t])](images/maple226.gif)
![[Maple Plot]](images/maple227.gif)
![[Maple Plot]](images/maple228.gif)
![[Maple Plot]](images/maple229.gif)
![[Maple Plot]](images/maple230.gif)
![[Maple Plot]](images/maple231.gif)
![[Maple Plot]](images/maple232.gif)
![[Maple Plot]](images/maple233.gif)
![[Maple Plot]](images/maple234.gif)
![[Maple Plot]](images/maple235.gif)
![[Maple Plot]](images/maple236.gif)
![[Maple Plot]](images/maple237.gif)
![[Maple Plot]](images/maple238.gif)
![[Maple Plot]](images/maple239.gif)
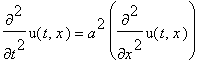
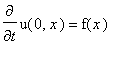 .
.
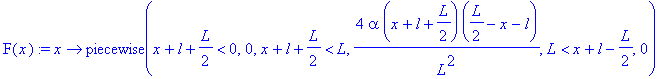
![[Maple Plot]](images/maple250.gif)
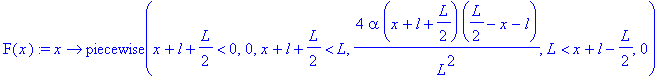
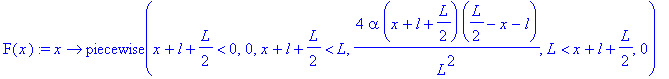
![u(t,x) := 1/2*PIECEWISE([0, x-a*t+l+1/2*L < 0],[4*alpha*(x-a*t+l+1/2*L)*(1/2*L-x+a*t-l)/L^2, x-a*t+l+1/2*L < L],[0, L < x-a*t+l+1/2*L])-1/2*PIECEWISE([0, x+a*t-l+1/2*L < 0],[4*alpha*(x+a*t-l+1/2*L)*(1/...](images/maple255.gif)
![u(t,x) := 1/2*PIECEWISE([0, x-a*t+l+1/2*L < 0],[4*alpha*(x-a*t+l+1/2*L)*(1/2*L-x+a*t-l)/L^2, x-a*t+l+1/2*L < L],[0, L < x-a*t+l+1/2*L])-1/2*PIECEWISE([0, x+a*t-l+1/2*L < 0],[4*alpha*(x+a*t-l+1/2*L)*(1/...](images/maple256.gif)
![u1(t,x) := 1/2*PIECEWISE([0, x-t < -5/2],[8*(x-t+5/2)*(-3/2-x+t), x-t < -3/2],[0, 0 < x-t+3/2])](images/maple261.gif)
![u2(t,x) := -1/2*PIECEWISE([0, x+t < 3/2],[8*(x+t-3/2)*(5/2-x-t), x+t < 5/2],[0, 0 < x+t-5/2])](images/maple262.gif)
![u(t,x) := 1/2*PIECEWISE([0, x-t < -5/2],[8*(x-t+5/2)*(-3/2-x+t), x-t < -3/2],[0, 0 < x-t+3/2])-1/2*PIECEWISE([0, x+t < 3/2],[8*(x+t-3/2)*(5/2-x-t), x+t < 5/2],[0, 0 < x+t-5/2])](images/maple264.gif)
![[Maple Plot]](images/maple265.gif)
![[Maple Plot]](images/maple266.gif)
![[Maple Plot]](images/maple267.gif)
![[Maple Plot]](images/maple268.gif)
 .
.
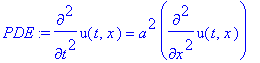
![struc := `&where`(u(t,x) = T(t)*X(x),[{diff(X(x),`$`(x,2)) = _c[1]*X(x)/a^2, diff(T(t),`$`(t,2)) = _c[1]*T(t)}])](images/maple275.gif)
![X(x) = _C1*exp(_c[1]^(1/2)/a*x)+_C2*exp(-_c[1]^(1/2)/a*x)](images/maple277.gif)
![u(t,x) := Sum((C1[n]*cos(Pi*n*a/L*t)+C2[n]*sin(Pi*n*a/L*t))*sin(Pi*n/L*x),n = 1 .. infinity)](images/maple290.gif)
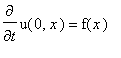 .
.
![Sum(C1[n]*sin(Pi*n/L*x),n = 1 .. infinity) = F(x)](images/maple295.gif)
![Sum(C2[n]*Pi*n*a/L*sin(Pi*n/L*x),n = 1 .. infinity) = f(x)](images/maple296.gif)
![C1[n] := 2/L*int(F(x)*sin(Pi*n/L*x),x = 0 .. L)](images/maple301.gif)
![C2[n] := 2/Pi/n/a*int(f(x)*cos(Pi*n/L*x),x = 0 .. L)](images/maple302.gif)
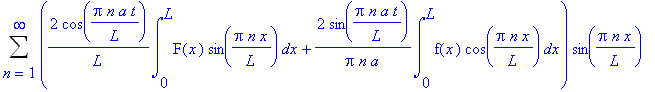
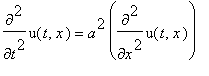
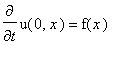 .
.
![[Maple Plot]](images/maple316.gif)
![C1[n] := -2*alpha*L*(sin(l*Pi*n/L)*L-l*sin(Pi*n))/l/Pi^2/n^2/(l-L)](images/maple319.gif)
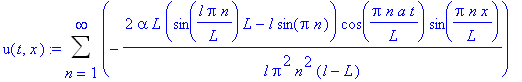
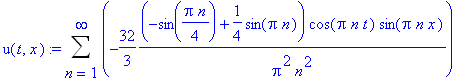
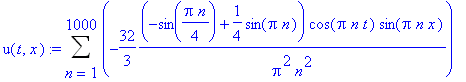
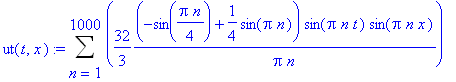
![[Maple Plot]](images/maple329.gif)
![[Maple Plot]](images/maple330.gif)
![[Maple Plot]](images/maple331.gif)
![[Maple Plot]](images/maple332.gif)
![[Maple Plot]](images/maple333.gif)
![[Maple Plot]](images/maple334.gif)
![[Maple Plot]](images/maple335.gif)
![[Maple Plot]](images/maple336.gif)
![[Maple Plot]](images/maple337.gif)
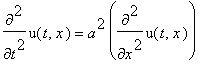
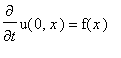 .
.
![[Maple Plot]](images/maple349.gif)
![C2[n] := -2/Pi^2/n^2/a*v0*L*(sin(Pi*n/L*l1)-sin(Pi*n/L*l2))](images/maple353.gif)
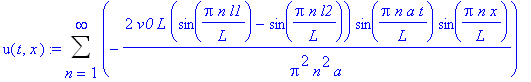
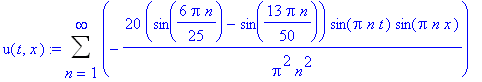
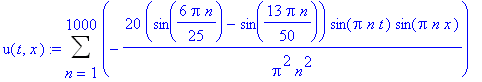
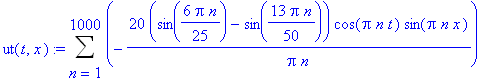
![[Maple Plot]](images/maple363.gif)
![[Maple Plot]](images/maple364.gif)
![[Maple Plot]](images/maple365.gif)
![[Maple Plot]](images/maple366.gif)
![[Maple Plot]](images/maple367.gif)
![[Maple Plot]](images/maple368.gif)
![[Maple Plot]](images/maple369.gif)
![[Maple Plot]](images/maple370.gif)
![[Maple Plot]](images/maple371.gif)
 .
.
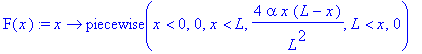
![[Maple Plot]](images/maple383.gif)
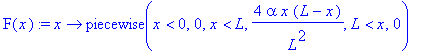
![C1[n] := -8*alpha*(-2+Pi*n*sin(Pi*n)+2*cos(Pi*n))/Pi^3/n^3](images/maple386.gif)
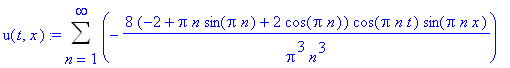
![[Maple Plot]](images/maple394.gif)
![[Maple Plot]](images/maple395.gif)
![[Maple Plot]](images/maple396.gif)
![[Maple Plot]](images/maple397.gif)
![[Maple Plot]](images/maple398.gif)
![[Maple Plot]](images/maple399.gif)
![[Maple Plot]](images/maple400.gif)
![[Maple Plot]](images/maple401.gif)
![[Maple Plot]](images/maple402.gif)
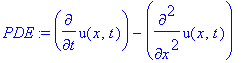
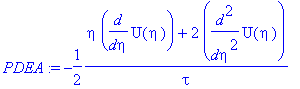
![[Maple Plot]](images/maple411.gif)
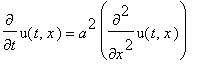
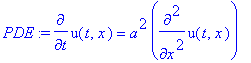
![struc := `&where`(u(t,x) = T(t)*X(x),[{diff(X(x),`$`(x,2)) = _c[1]*X(x)/a^2, diff(T(t),t) = _c[1]*T(t)}])](images/maple415.gif)
![X(x) = _C1*exp(_c[1]^(1/2)/a*x)+_C2*exp(-_c[1]^(1/2)/a*x)](images/maple417.gif)
 := (C1(lambda)*sin(lambda*x)+C2(lambda)*cos(lambda*x))*exp(-lambda^2*a^2*t)](images/maple431.gif)
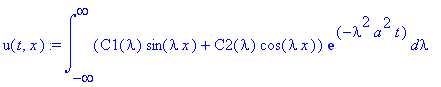
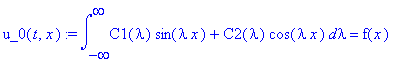
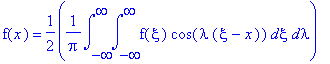
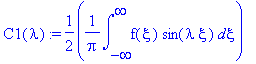
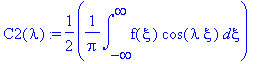
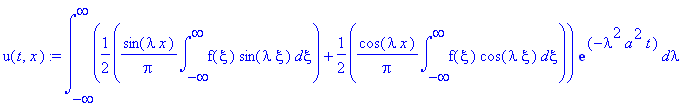
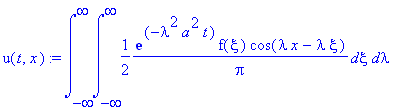
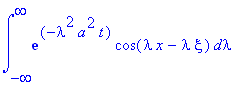
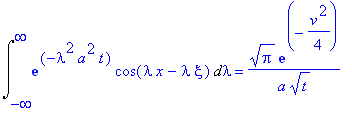
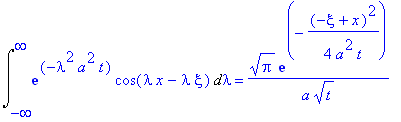
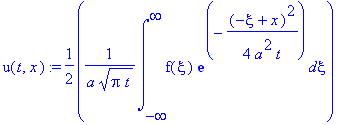
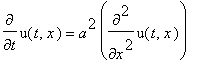
![[Maple Plot]](images/maple459.gif)
![u(t,x) := 1/2*1/(Pi*t)^(1/2)*PIECEWISE([2*exp(1/(-4*gamma^2*t-1)*x^2*gamma^2)*u0/((4*gamma^2*t+1)/t)^(1/2)*Pi^(1/2), csgn(gamma^2+1/(4*t)) = 1],[infinity, otherwise])](images/maple460.gif)
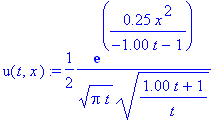
![[Maple Plot]](images/maple465.gif)
![[Maple Plot]](images/maple466.gif)
![[Maple Plot]](images/maple467.gif)
![[Maple Plot]](images/maple468.gif)
![[Maple Plot]](images/maple469.gif)
![[Maple Plot]](images/maple470.gif)
![[Maple Plot]](images/maple471.gif)
![[Maple Plot]](images/maple472.gif)
![[Maple Plot]](images/maple473.gif)
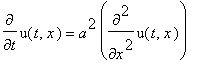
![[Maple Plot]](images/maple481.gif)
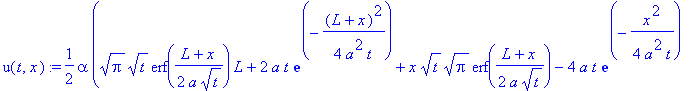
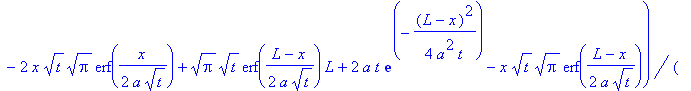
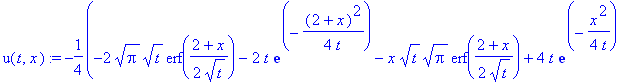
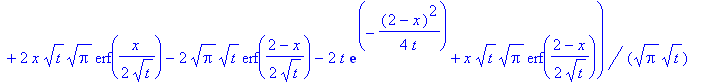
![[Maple Plot]](images/maple491.gif)
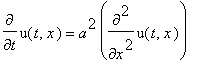
![[Maple Plot]](images/maple499.gif)
![[Maple Plot]](images/maple506.gif)
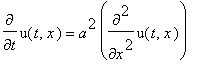
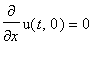 .
.
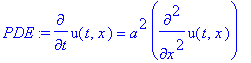
![struc := `&where`(u(t,x) = T(t)*X(x),[{diff(X(x),`$`(x,2)) = _c[1]*X(x)/a^2, diff(T(t),t) = _c[1]*T(t)}])](images/maple514.gif)
![X(x) = _C1*exp(_c[1]^(1/2)/a*x)+_C2*exp(-_c[1]^(1/2)/a*x)](images/maple516.gif)
 := (C1(lambda)*sin(lambda*x)+C2(lambda)*cos(lambda*x))*exp(-lambda^2*a^2*t)](images/maple530.gif)
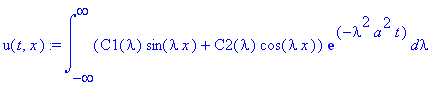
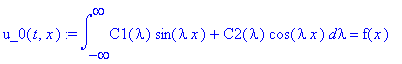
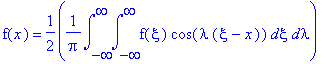
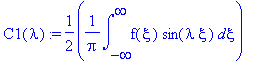
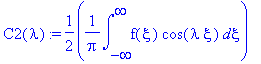
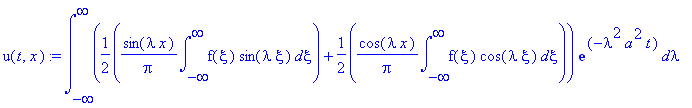
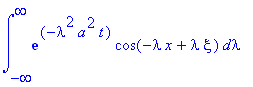
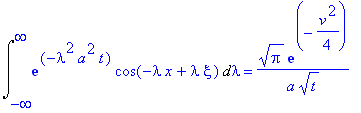
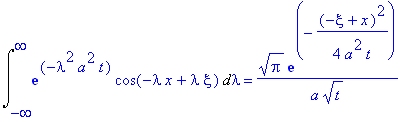
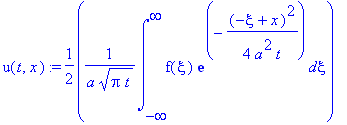
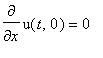 .
.
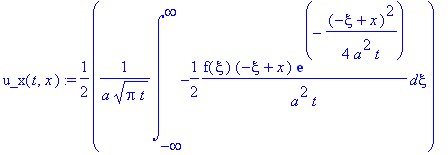
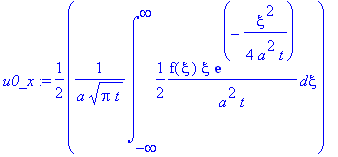
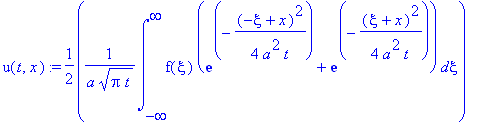
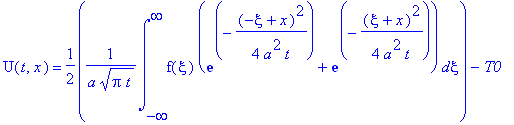
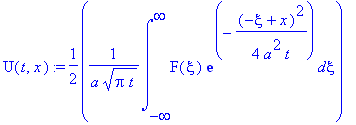
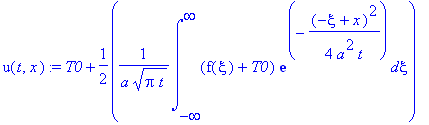
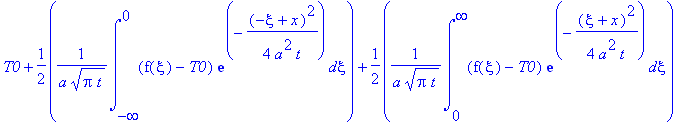
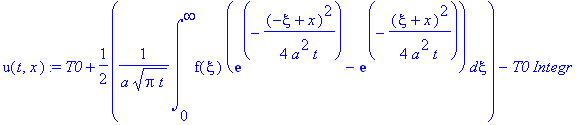
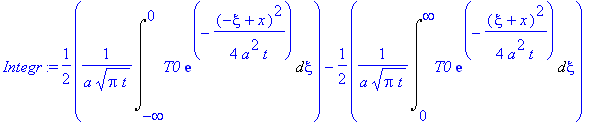
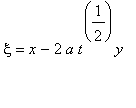 ,
,
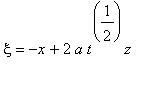 .
.
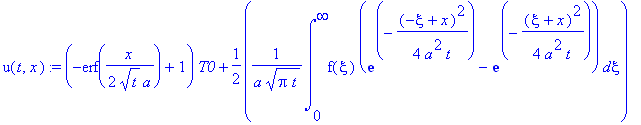
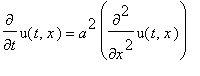
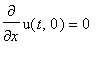 .
.
![[Maple Plot]](images/maple592.gif)
![[Maple Plot]](images/maple600.gif)
![[Maple Plot]](images/maple601.gif)
![[Maple Plot]](images/maple602.gif)
![[Maple Plot]](images/maple603.gif)
![[Maple Plot]](images/maple604.gif)
![[Maple Plot]](images/maple605.gif)
![[Maple Plot]](images/maple606.gif)
![[Maple Plot]](images/maple607.gif)
![[Maple Plot]](images/maple608.gif)
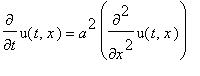
![[Maple Plot]](images/maple621.gif)
![[Maple Plot]](images/maple630.gif)
![[Maple Plot]](images/maple631.gif)
![[Maple Plot]](images/maple632.gif)
![[Maple Plot]](images/maple633.gif)
![[Maple Plot]](images/maple634.gif)
![[Maple Plot]](images/maple635.gif)
![[Maple Plot]](images/maple636.gif)
![[Maple Plot]](images/maple637.gif)
![[Maple Plot]](images/maple638.gif)
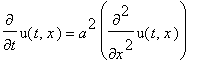
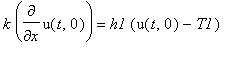
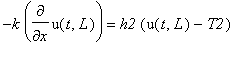
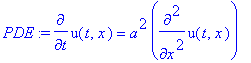
![struc := `&where`(u(t,x) = T(t)*X(x),[{diff(X(x),`$`(x,2)) = _c[1]*X(x)/a^2, diff(T(t),t) = _c[1]*T(t)}])](images/maple649.gif)
![X(x) = _C1*exp(_c[1]^(1/2)/a*x)+_C2*exp(-_c[1]^(1/2)/a*x)](images/maple651.gif)
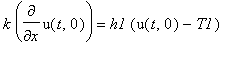
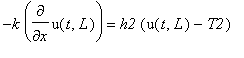
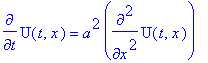
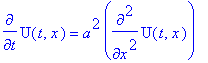
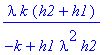
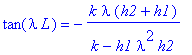
 := (C1[n]*sin(lambda[n]*x)+C2[n]*cos(lambda[n]*x))*exp(-lambda[n]^2*a^2*t)](images/maple718.gif)
 := (C1[n]*sin(Pi*n/L*x)+C2[n]*cos(Pi*n/L*x))*exp(-Pi^2*n^2/L^2*a^2*t)](images/maple720.gif)
 := (C1[n]*cos(Pi*n/L*x)*Pi*n/L-C2[n]*sin(Pi*n/L*x)*Pi*n/L)*exp(-Pi^2*n^2/L^2*a^2*t)](images/maple721.gif)
![C1[n]*Pi*n/L*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple722.gif)
![(C1[n]*cos(Pi*n)*Pi*n/L-C2[n]*sin(Pi*n)*Pi*n/L)*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple723.gif)
![C1[n]*(-1)^n*Pi*n/L*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple724.gif)
 := C2[n]*cos(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t)](images/maple726.gif)
![U(t,x) := sum(C2[n]*cos(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t),n = 0 .. infinity)](images/maple727.gif)
![sum(C2[n]*cos(Pi*n/L*x),n = 0 .. infinity) = F(x)](images/maple728.gif)
![C2[n] := 2/L*int(F(xi)*cos(Pi*n/L*xi),xi = 0 .. L)](images/maple730.gif)
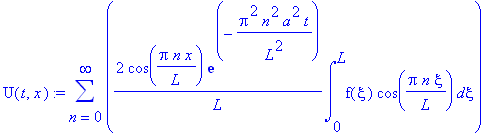
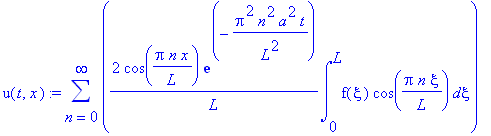
 := (C1[n]*sin(Pi*n/L*x)+C2[n]*cos(Pi*n/L*x))*exp(-Pi^2*n^2/L^2*a^2*t)](images/maple735.gif)
![C2[n]*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple736.gif)
![(C1[n]*sin(Pi*n)+C2[n]*cos(Pi*n))*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple737.gif)
![C2[n]*(-1)^n*exp(-Pi^2*n^2/L^2*a^2*t)*k = 0](images/maple738.gif)
 := C1[n]*sin(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t)](images/maple740.gif)
![U(t,x) := sum(C1[n]*sin(Pi*n/L*x)*exp(-Pi^2*n^2/L^2*a^2*t),n = 0 .. infinity)](images/maple741.gif)
![sum(C1[n]*sin(Pi*n/L*x),n = 0 .. infinity) = F(x)](images/maple742.gif)
![C1[n] := 2/L*int(F(xi)*cos(Pi*n/L*xi),xi = 0 .. L)](images/maple744.gif)
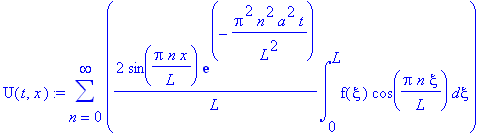
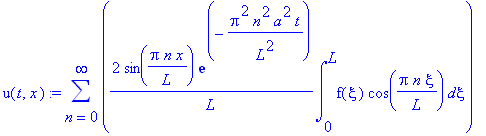
 := (C1[n]*sin(1/2*Pi*(1+2*n)/L*x)+C2[n]*cos(1/2*Pi*(1+2*n)/L*x))*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)](images/maple749.gif)
 := (1/2*C1[n]*cos(1/2*Pi*(1+2*n)/L*x)*Pi*(1+2*n)/L-1/2*C2[n]*sin(1/2*Pi*(1+2*n)/L*x)*Pi*(1+2*n)/L)*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)](images/maple751.gif)
![1/2*C1[n]*Pi*(1+2*n)/L*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)*k = 0](images/maple752.gif)
![(C1[n]*sin(1/2*Pi*(1+2*n))+C2[n]*cos(1/2*Pi*(1+2*n)))*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)*k = 0](images/maple753.gif)
![C1[n]*(-1)^n*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)*k = 0](images/maple754.gif)
 := C2[n]*cos(1/2*Pi*(1+2*n)/L*x)*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t)](images/maple756.gif)
![U(t,x) := sum(C2[n]*cos(1/2*Pi*(1+2*n)/L*x)*exp(-1/4*Pi^2*(1+2*n)^2/L^2*a^2*t),n = 1 .. infinity)](images/maple757.gif)
![sum(C2[n]*cos(1/2*Pi*(1+2*n)/L*x),n = 1 .. infinity) = F(x)](images/maple758.gif)
![C2[n] := 2/L*int(F(xi)*cos(1/2*Pi*(1+2*n)/L*xi),xi = 0 .. L)](images/maple760.gif)
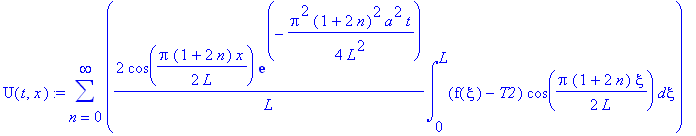
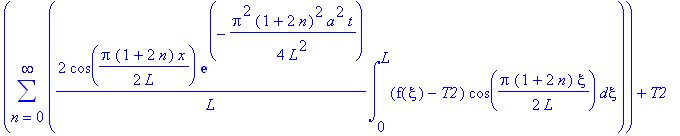
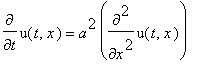
![[Maple Plot]](images/maple775.gif)
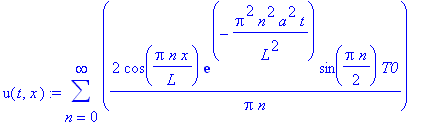
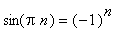 при
при
![[Maple Plot]](images/maple789.gif)
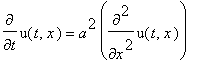
![[Maple Plot]](images/maple797.gif)
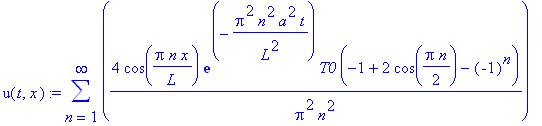
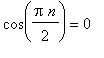 при
при
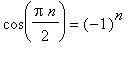 при
при
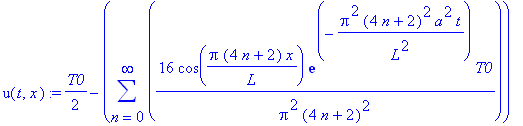
![[Maple Plot]](images/maple813.gif)
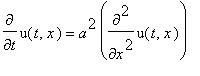
![[Maple Plot]](images/maple821.gif)
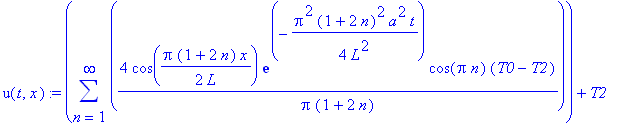
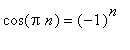
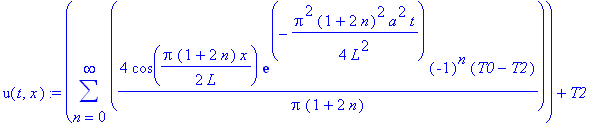
![[Maple Plot]](images/maple830.gif)